Доверительный интервал для математического ожидания генеральной совокупности, имеющей нормальное распределение при известной дисперсии.
Пусть из генеральной совокупности X, имеющей нормальный закон распределения при известной дисперсии 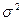 и неизвестном математическом ожидании
и неизвестном математическом ожидании 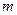 , произведена случайная выборка
, произведена случайная выборка 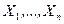 . Для оценки математического ожидания используем статистику
. Для оценки математического ожидания используем статистику 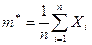 , которая имеет нормальное распределение с параметрами
, которая имеет нормальное распределение с параметрами 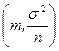 . Тогда статистика
. Тогда статистика 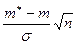 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами  . Найдем вероятность отклонения
. Найдем вероятность отклонения 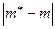 :
:
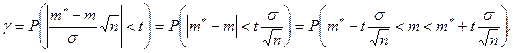 (8.4.5)
(8.4.5)
Интервал 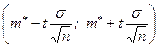 , определенный по (8.4.5), представляет собой доверительный интервал для математического ожидания
, определенный по (8.4.5), представляет собой доверительный интервал для математического ожидания 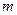 при известной дисперсии
при известной дисперсии 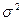 . Осталось указать, как, зная доверительную вероятность
. Осталось указать, как, зная доверительную вероятность 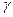 , выбрать в (8.4.5) значение
, выбрать в (8.4.5) значение 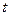 . Ответом на этот вопрос является доказанная ранее теорема, т.е.
. Ответом на этот вопрос является доказанная ранее теорема, т.е. 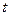 является квантилем уровня
является квантилем уровня 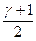 нормального распределения с параметрами
нормального распределения с параметрами  .
.
Таким образом, доверительный интервал для математического ожидания 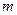 при известной дисперсии
при известной дисперсии 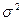 строится следующим образом:
строится следующим образом:
1. Вычисляем оценку 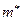 , которая является средним арифметическим элементов выборки
, которая является средним арифметическим элементов выборки 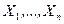 .
.
2. Вычисляем квантиль 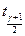 нормального распределения с параметрами
нормального распределения с параметрами  .
.
3. Строим доверительный интервал, который имеет вид:
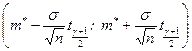 .(8.4.6)
.(8.4.6)
Очевидно, что точность оценки равна
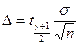 . (8.4.7)
. (8.4.7)
Замечание. Квантиль 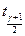 нормального распределения с параметрами
нормального распределения с параметрами  можно определить разными способами, например:
можно определить разными способами, например:
§ используя таблицы функции 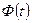 нормального распределения с параметрами
нормального распределения с параметрами  (Приложение 3);
(Приложение 3);
§ используя функцию НОРМСТОБР(вероятность) из EXCEL, при этом аргумент «вероятность» данной функции должен быть равен 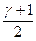 ;
;
§ используя функцию qnorm(ν, m, σ) из MATHCAD, при этом переменные данной функции должны быть равны 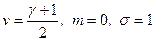 .
.
Дата добавления: 2015-05-28; просмотров: 1000;
