Точечные оценки. Выборочная средняя и выборочная дисперсия

Пусть 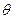— некоторый параметр закона распределения генеральной совокупности.

Определение. Точечной оценкой 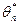параметра 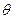называется произвольная функция 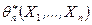случайной выборки .

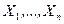Статическая оценка является случайной величиной и меняется в зависимости от выборки. Опишем свойства, которым должна удовлетворять оценка .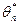

Определение. Оценка 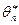называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т.е.

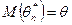. (8.1.1)

Определение. Оценка 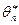называется состоятельной, если с ростом объема выборки она сходится к оцениваемому параметру. Можно рассматривать сходимость различных типов: по вероятности, с вероятностью равной единице, в среднем квадратичном и т.д. Как правило, рассматривается сходимость по вероятности, т.е. состоятельной называется оценка 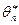, которая для каждого 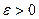при всех возможных значениях неизвестного параметра 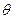удовлетворяет соотношению

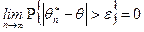. (8.1.2)

Определение. Несмещенная оценка 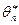называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра 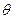, вычисленных по случайным выборкам одного и того же объема.

Если оценка не является несмещенной, то она будет либо завышать значение 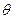, либо занижать его. В обоих случаях это приводит к систематическим ошибкам одного знака в оценке параметра 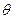. Состоятельность оценки обосновывает увеличение объема случайной выборки, так как при этом становится менее вероятной возможность большой ошибки в оценке параметра .

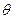Замечание.В дальнейшем вместо обозначения 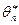будем использовать .

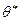Определение.Выборочной средней называется среднее арифметическое полученных по выборке значений

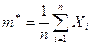. (8.1.3)

Определение. Вторым выборочным моментом называется среднее арифметическое квадратов, полученных по выборке значений

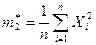. (8.1.4)

Определение. Выборочной дисперсией называется среднее арифметическое квадратов отклонений значений в случайной выборке от выборочной средней

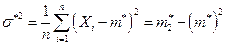. (8.1.5)

Определение. Исправленной выборочной дисперсией называется произведение выборочной дисперсии на величину 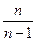, т.е.

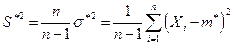. (8.1.6)

Пример 1. Проверить, является ли второй выборочный момент 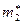несмещенной оценкой второго теоретического момента.

m Решение.Найдем математическое ожидание оценки .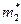

L

Пример 2. Проверить, является ли оценка 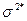несмещенной.