Эмпирическая функция распределения
По статистическом ряду, приведенному в таблице 7.3,
Таблица 7.3
| № | … | 
| ||
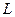
Варианты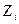 
| 
| 
| … | 
|
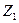
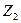
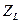
Относительная частота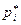 
| 
| 
| … | 
|
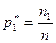
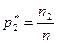
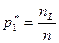
можно построить эмпирическую (выборочную) функцию распределения.
Определение. Эмпирической (выборочной) функцией распределения называется функция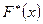 
, задающая для каждого значения 
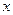относительную частоту события 
.
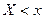Следовательно, по определению
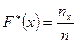, (7.3.1)
где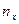 
— число элементов выборки, значения которых меньше .
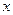Очевидно, что для нахождения функции распределения можно использовать формулу
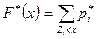. (7.3.2)
Эмпирическую функцию распределения можно задать таблично или графически. Построим эмпирическую функцию распределения по данным, приведенным в таблице 7.2.
Объем выборки по условию примера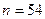 
. Наименьшая варианта равна 0, следовательно, 
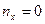при 
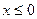. Тогда 
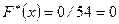при 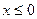. Если 
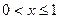, то неравенство 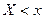выполняется для варианты 
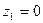, которая встречается 31 раз, поэтому 
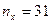и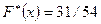 
. Если 
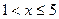, то неравенство 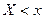выполняется для вариант 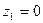и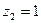 
, которые встречаются 31 и 14 раз соответственно, поэтому, 
, 
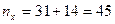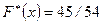и т.д. Результаты вычисления 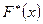приведем в таблице 7.4
Таблица 7.4
|
|
|
|
| |
|
| 
|
|
| 
|
| 
|
| 
|
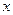
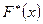
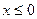
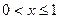
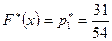
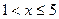
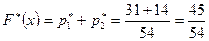
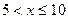
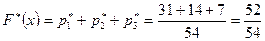
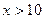
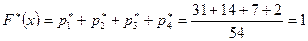
График этой функции приведен на рис. 7.1.
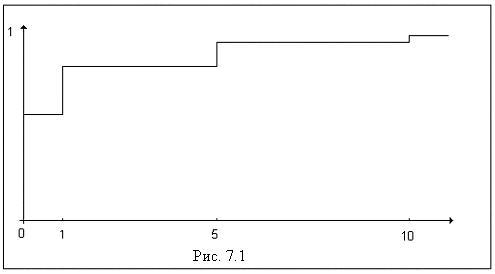
В случае интервального ряда значения эмпирической функции 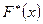подсчитывают на концах частичных интервалов.
Эмпирическая функция 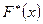применяется для оценивания теоретической функции распределения генеральной совокупности.
Дата добавления: 2015-05-28; просмотров: 1120;