Полигон и гистограмма

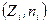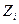Определение. Полигоном частот (многоугольником распределения)называется ломаная линия, проходящая через точки с координатами , где — варианты статистического ряда, а 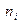— соответствующие им частоты.

Если ломаная линия строится по точкам 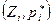, где — относительные частоты, то получаем полигон относительных частот.

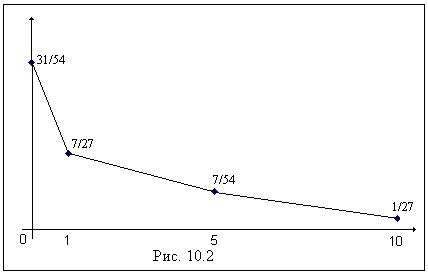
Построим полигон относительных частот для выборки из примера 2. Используя статистический ряд, представленный в таблице 7.2, получаем полигон относительных частот, изображенный на рис. 7.2.

В случае непрерывной случайной величины выборку преобразуют следующим образом. Всю ось абсцисс делят на интервал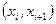ы длины 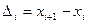и определяют функцию 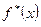, которая на 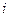‑м интервале принимает значение

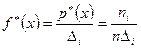, (7.4.1)

где 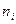— число элементов выборки, попавших в интервал.