Гистограмма распределения
Одной из главных проблем при проведении многократных измерений одной и той же величины является представление результатов измерений. Один из удобных методов представления результатов - построение гистограмм распределений. Гистограмма распределения строится следующим образом. После того, как получена таблица измеренных значений, в качестве первого шага нужно переписать её в порядке возрастания значений измеренной величины, чтобы было удобно проанализировать полученные результаты наблюдений. Например, результаты 100 измерений, приведенные в табл. 4.1, после расположения в порядке возрастания представлены в табл. 4.4.
Таблица 4.4. Упорядоченные значения 100 первых результатов измерений из табл. 4.1.
После того, как составлена таблица упорядоченных в порядке возрастания значений результатов измерений  , на следующем шаге строится эмпирическое распределение результатов измерений. Для этого результаты измерений должны быть сгруппированы.
, на следующем шаге строится эмпирическое распределение результатов измерений. Для этого результаты измерений должны быть сгруппированы.
Пусть имеется таблица значений nmin, ..., nmax. Положим С1 равным наименьшему значению nmin и Сk - наибольшему nmax.
Разобьем отрезок [С1 ,Сk] на k равных интервалов группировки (при ста измерениях можно взять k = 10 - 12). Длина каждого интервала группировки DL будет равна
 . (4.28)
. (4.28)
Для нашего примера возьмем k=10, тогда 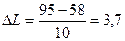 . Так как число интервалов разбиения произвольно, в качестве ширины интервала для удобства возьмем
. Так как число интервалов разбиения произвольно, в качестве ширины интервала для удобства возьмем  .
.
Обозначим начало каждого интервала 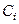 , конец интервала
, конец интервала  (i=1,...,k). Подсчитаем число наблюдений
(i=1,...,k). Подсчитаем число наблюдений 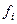 (i=1,...,k) из набора значений (n1 ,..., nN), лежащих в каждом интервале [Сi, Сi+1):
(i=1,...,k) из набора значений (n1 ,..., nN), лежащих в каждом интервале [Сi, Сi+1):
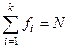 . (4.29)
. (4.29)
Определим относительные частоты наблюдений pi
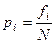 ,
,  . (4.30)
. (4.30)
Для построения гистограммы составляют таблицу частоты наблюдений 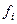 сгруппированных величин
сгруппированных величин  (табл. 4.5).
(табл. 4.5).
Для рассмотренного нами случая C1=58, Ck+1=96.
| Табл. 4.5. Относительные частоты наблюдений pi сгруппированных величин ni. | ||
| Интервал | Число наблюдений, fi | Относительная частота наблюдений, pi |
| [C1, С2) [С2, С3) … [Сk, Сk+1] | f1 f2 … fk | p1 p2 … pk |
Итак, в первый интервал попало 3 значения измеренной величины: 58, 60, 60, во второй – 3 значения: 64, 65, 66, в третий – 11 значений. Таким образом относительная частота наблюдений в первом интервале равна 0,03, во втором – 0,03, в третьем – 0,11, и т.д.
Графическое изображение зависимости относительной частоты наблюдений pi от соответствующего интервала группировки называется гистограммой выборки (рис. 4.6). Таким образом, эмпирическая функция плотности распределения определяется следующим выражением:
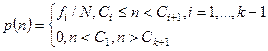 . (4.31)
. (4.31)
| Табл. 4.6. Относительные частоты наблюдений pi величин ni для измерений, приведенных в таблице 1. | |||
| Интервал | Интервал | Число наблюдений, fi | Относительная частота наблюдений, pi |
| [С1 , С2) | [58,62 ) | 0,03 | |
| [С2 , С3) | [62,66 ) | 0,03 | |
| [С3 , С4) | [66,70 ) | 0,11 | |
| [С4 , С5) | [70,74 ) | 0,16 | |
| [С5 , С6) | [74,78 ) | 0,20 | |
| [С6 , С7) | [78,82 ) | 0,15 | |
| [С7 , С8) | [82,86 ) | 0,13 | |
| [С8 , С9) | [86,90 ) | 0,10 | |
| [С9 , С10) | [90,94 ) | 0,06 | |
| [С10 , С11] | [94,98 ) | 0,03 |
 Так как длина интервала при построении гистограмм выбирается одинаковой, то высота каждого столбца гистограммы оказывается пропорциональной частоте наблюдений (рис. 4.6). Ясно, что выбор величины интервала ∆L существенно влияет на общий вид гистограммы. Если длина интервала ∆L мала, то влияние случайных колебаний числа наблюдений в каждом интервале начинает преобладать, т. к. каждый интервал содержит при этом лишь небольшое число наблюдений, причем возможная дисперсия числа наблюдений в каждом интервале приблизительно равна этому числу. Но чем больше величина ∆L, тем более скрадываются характерные черты распределения. Поэтому оптимальное число интервалов k должно удовлетворять приближенным требованиям:
Так как длина интервала при построении гистограмм выбирается одинаковой, то высота каждого столбца гистограммы оказывается пропорциональной частоте наблюдений (рис. 4.6). Ясно, что выбор величины интервала ∆L существенно влияет на общий вид гистограммы. Если длина интервала ∆L мала, то влияние случайных колебаний числа наблюдений в каждом интервале начинает преобладать, т. к. каждый интервал содержит при этом лишь небольшое число наблюдений, причем возможная дисперсия числа наблюдений в каждом интервале приблизительно равна этому числу. Но чем больше величина ∆L, тем более скрадываются характерные черты распределения. Поэтому оптимальное число интервалов k должно удовлетворять приближенным требованиям:
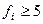 ,
, 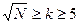 (N - объем выборки).
(N - объем выборки).
После того, как гистограмма построена, необходимо рассчитать экспериментальные значения 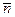 и
и 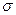 .
.
Чтобы установить, является ли распределение случайной величины n нормальным, на график эмпирической функции плотности распределения 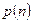 накладывают вычисленную кривую нормального распределения с параметрами
накладывают вычисленную кривую нормального распределения с параметрами  и
и 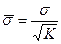 .
.
На рис. 4.6 гистограмма распределения активности радиоактивного источника, сравнивается с распределением Гаусса с параметрами 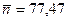 и
и  , приведенными в таблице 4.6.
, приведенными в таблице 4.6.
Выше мы изложили формальную схему построения таблицы данных для определения частоты наблюдения fi величины n. Однако может случиться так, что при измерении величин ni одно из значений окажется сильно отличающимся (на несколько 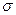 ) от среднего значения. В этом случае при определении интервала разбиения
) от среднего значения. В этом случае при определении интервала разбиения  согласно соотношению (4.28) необходимо в качестве верхней Ck+1 или нижней Ck границы интервала выбрать результат измерения, отличающийся на одно измерение.
согласно соотношению (4.28) необходимо в качестве верхней Ck+1 или нижней Ck границы интервала выбрать результат измерения, отличающийся на одно измерение.
Таким образом, при построении гистограммы распределений, при выборе числа интервалов группировки и границ интервалов группировки, необходимо руководствоваться «здравым смыслом».
В том случае, когда строится гистограмма распределения Пуассона для малых значений 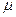 , необходимо просто сосчитать число измерений с n=0, n=1,…и так далее до n=nmax, и далее рассчитать относительные частоты, пользуясь соотношением (34.0).
, необходимо просто сосчитать число измерений с n=0, n=1,…и так далее до n=nmax, и далее рассчитать относительные частоты, пользуясь соотношением (34.0).
Дата добавления: 2015-05-16; просмотров: 2220;
