Статистические и систематические ошибки измерений
Целью каждого измерения является определение значения некоторой величины. Однако из-за различных неточностей процесса измерения результаты измерений в общем случае отличаются от искомого точного значения. При оценке результатов измерения обычно исходят из того, что измерения можно повторить многократно. Условия проведения измерений при этом не должны изменяться.
Опыт показывает, что любое измерение, как бы аккуратно оно не проводилось, не может быть совершенно свободно от ошибок. В научных исследованиях слово «ошибка» означает неизбежную погрешность, которой сопровождаются все измерения. Ошибка измерения характеризует точность, с которой выполнено измерение. Ошибки измерений обусловлены большим количеством разнообразных причин. В некоторых случаях удается выделить причины этих ошибок и внести необходимую поправку в результат измерений. Так, например, если после проведения экспериментов была обнаружена неправильная калибровка прибора, которая привела к смещению начала отсчета измеряемой величины, и если шкала отсчетов линейная, то все измеренные показания необходимо сместить на эту обнаруженную ошибку измерений.
Другой причиной погрешностей эксперимента может быть неточность прибора, измеряющего временной интервал наблюдения. Например, если используемый секундомер постоянно отстает, то все измеренные значения времени будут недооценены и никакое количество повторений измерений с тем же секундомером не обнаружит этот источник ошибок. Для того чтобы максимально избежать таких ошибок в научных экспериментах стараются использовать специально калиброванные приборы.
Принято говорить, что каждая из таких причин вызывает систематическую ошибку измерений. Как только систематические ошибки обнаружены и их величины рассчитаны, они могут быть устранены внесением соответствующих поправок в результаты измерений. Однако необходимо помнить, что общая ошибка каждого результата измерения остается неизвестной, т.к. речь идет не о выделении из общей ошибки наблюдения некоторой ее части в виде систематической ошибки, а лишь о введении поправок на те факторы, которые удалось выявить в процессе анализа результатов эксперимента. Правильная оценка систематических ошибок в значительной степени зависит от опыта экспериментатора и его способности критически смотреть на полученные результаты. Наряду с систематическими ошибками существуют и другого типа ошибки - статистические.
Экспериментальные погрешности, которые можно обнаружить с помощью многократных измерений, называются случайными или статистическими ошибками. В ядерной физике и физике частиц процессы являются принципиально статистическими. Поэтому случайные ошибки играют очень большую роль.
Эту особенность процессов, происходящих в микромире, легко понять, наблюдая за распадом радиоактивных ядер, каждое из которых распадается независимо от любого другого. Нельзя предсказать, когда именно распадется данное нестабильное ядро. Для описания статистических закономерностей используется понятие вероятности события.
Естественной статистической величиной, описывающей радиоактивный распад, является вероятность распада 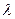 ядра за единицу времени. Независимость величины
ядра за единицу времени. Независимость величины 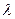 от времени выражается в том, что различные моменты времени ничем не выделены друг относительно друга с точки зрения вероятности предстоящего распада ядер.
от времени выражается в том, что различные моменты времени ничем не выделены друг относительно друга с точки зрения вероятности предстоящего распада ядер.
Статистические ошибки являются неустранимыми - их нельзя исключить в каждом из результатов измерений. Но с помощью методов теории вероятности можно учесть их влияние на оценку истинного значения измеряемой величины, что позволяет определить значение измеряемой величины со значительно меньшей ошибкой, чем ошибки отдельных измерений. Учёт влияния статистических ошибок основан на знании законов их распределения, т.к. статистические ошибки измерения характеризуются определенным законом распределения. Существование такого закона можно обнаружить, повторяя много раз в неизменных условиях измерения некоторой величины.
Рассмотрим эксперимент по определению активности радиоактивного источника. Выберем такой случай, когда активность источника не меняется в течение времени наблюдения, т.е. выберем в качестве источника моноизотопный радиоактивный источник, среднее время жизни которого 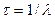 много больше времени отдельных наблюдений ti и полного времени всех наблюдений T. Эксперимент заключается в том, что с помощью детектора регистрируется число частиц
много больше времени отдельных наблюдений ti и полного времени всех наблюдений T. Эксперимент заключается в том, что с помощью детектора регистрируется число частиц 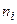 , образующихся в результате распада радиоактивного источника. Интервал времени ti, в течение которого проводится каждое отдельное наблюдение, фиксирован (ti= 1 с). Результаты измерений приведены в табл. 1.
, образующихся в результате распада радиоактивного источника. Интервал времени ti, в течение которого проводится каждое отдельное наблюдение, фиксирован (ti= 1 с). Результаты измерений приведены в табл. 1.
Всего было выполнено 100 независимых измерений в идентичных условиях. Видно, что в каждом отдельном измерении регистрируется какое-то количество случайных отсчетов, никак не связанных с результатами предыдущих измерений.
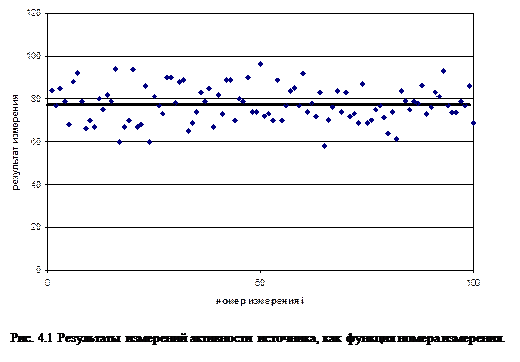
На рис. 4.1 показаны результаты этих измерений, как функция номера измерения i. Видно, что они сконцентрированы вблизи некоторой величины  . Среднее число частиц
. Среднее число частиц  , зарегистрированных в результате N измерений, определяется формулой
, зарегистрированных в результате N измерений, определяется формулой
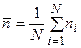 . (4.1)
. (4.1)
В нашем случае N = 100,  =77,47. Величина
=77,47. Величина  =77,47 показана на рис. 4.1 жирной линией.
=77,47 показана на рис. 4.1 жирной линией.
Очевидно, что усредненная по N измерениям величина активности  будет гораздо точнее характеризовать активность источника, чем результаты отдельных измерений.
будет гораздо точнее характеризовать активность источника, чем результаты отдельных измерений.
Несмотря на то, что в среднем все результаты измерений концентрируются вблизи  , тем не менее, результаты отдельных измерений отличаются от
, тем не менее, результаты отдельных измерений отличаются от  , как это и следовало ожидать, учитывая случайный характер наблюдаемых событий.
, как это и следовало ожидать, учитывая случайный характер наблюдаемых событий.
Возникает вопрос, как располагаются различные значения 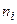 вокруг
вокруг  ? В целом, ответ на этот вопрос можно получить, используя более детальное описание распределения вероятности их наблюдения в окрестности среднего значения (см. далее). В первом приближении, можно использовать следующую процедуру.
? В целом, ответ на этот вопрос можно получить, используя более детальное описание распределения вероятности их наблюдения в окрестности среднего значения (см. далее). В первом приближении, можно использовать следующую процедуру.
Если считать, что  - это наилучшая оценка величин
- это наилучшая оценка величин 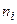 , то естественно рассмотреть разность
, то естественно рассмотреть разность
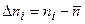 .
.
Величина 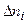 называется отклонением от средней величины
называется отклонением от средней величины  .
.
Для нашего примера величина отклонения для каждого отдельного измерения приведена в табл. 4.1. Чтобы попытаться оценить достоверность результатов, казалось, можно было бы поступить аналогично и усреднить величины 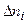 , однако, усредненная
, однако, усредненная 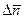 величина равна нулю. Так будет для любых измерений, что следует из самого определения величины
величина равна нулю. Так будет для любых измерений, что следует из самого определения величины 
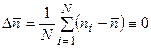 . (4.2)
. (4.2)
Чтобы обойти эту неприятность, в статистике используют другую величину, равную квадрату отклонения, усредненному по всевозможным значениям этой величины, которая называется дисперсией и обозначается символом D. Квадратный корень из дисперсии называется стандартным отклонением 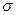 :
:
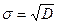 . (4.3)
. (4.3)
Таблица 4.1. Результаты измерений активности радиоактивного препарата.
| Номер измерения i | Результат измерения | Отклонение от среднего | Номер измерения i | Результат измерения | Отклонение от среднего | Номер измерения i | Результат измерения | Отклонение от среднего |
| 6.53 | -3.47 | -3.47 | ||||||
| -0.47 | 5.53 | 5.53 | ||||||
| 7.53 | 1.53 | -5.47 | ||||||
| 1.53 | 7.53 | -4.47 | ||||||
| -9.47 | -10.47 | -8.47 | ||||||
| 10.53 | 4.53 | 9.53 | ||||||
| 14.53 | -4.47 | -8.47 | ||||||
| 1.53 | 11.53 | -7.47 | ||||||
| -11.47 | 11.53 | -2.47 | ||||||
| -7.47 | -7.47 | -0.47 | ||||||
| -10.47 | 2.53 | -6.47 | ||||||
| 2.53 | 1.53 | -13.47 | ||||||
| -2.47 | 12.53 | -3.47 | ||||||
| 4.53 | -3.47 | -16.47 | ||||||
| 1.53 | -3.47 | 6.53 | ||||||
| 16.53 | 18.53 | 1.53 | ||||||
| -17.47 | -5.47 | -2.47 | ||||||
| -10.47 | -4.47 | 1.53 | ||||||
| -7.47 | -7.47 | 0.53 | ||||||
| 16.53 | 11.53 | 8.53 | ||||||
| -10.47 | -7.47 | -4.47 | ||||||
| -9.47 | -0.47 | -1.47 | ||||||
| 8.53 | 6.53 | 5.53 | ||||||
| -17.47 | 7.53 | 3.53 | ||||||
| 3.53 | -0.47 | 15.53 | ||||||
| -0.47 | 14.53 | -0.47 | ||||||
| -4.47 | -3.47 | -3.47 | ||||||
| 12.53 | 0.53 | -3.47 | ||||||
| 12.53 | -5.47 | 1.53 | ||||||
| 0.53 | 5.53 | -0.47 | ||||||
| 10.53 | -19.47 | 8.53 | ||||||
| 11.53 | -7.47 | -8.47 | ||||||
| -12.47 | -1.47 | |||||||
| -8.47 | 6.53 |
Стандартное отклонение 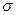 характеризует среднюю погрешность отдельных измерений
характеризует среднюю погрешность отдельных измерений 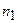 ,
, 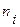 , …,
, …, 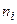 , …,
, …, 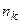 , поскольку оно указывает вероятность обнаружения наблюдаемых значений в интервале
, поскольку оно указывает вероятность обнаружения наблюдаемых значений в интервале 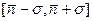 .
.
Практически, для этого возводят в квадрат все отклонения от средней величины и затем эти величины усредняют:
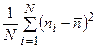 . (4.4)
. (4.4)
Однако обычно определение (4.4) «модифицируется» так, что в знаменателе вместо N стоит N-1, т.е.
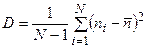 . (4.5)
. (4.5)
Эта величина является дисперсией измерения, которая является точной при N >> 1.
Причина «модификации» при вычислении дисперсии заключается в следующем. Определение (4.5) приводит к несколько большему значению дисперсии, чем (4.4), и это частично компенсирует ошибку в измерениях в том случае, когда число измерений мало. Понять это можно, если рассмотреть предельный случай одного измерения N=1. В этом случае из формул (4.1) и (4.4) следует 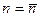 и D = 0. Т.е. получается явно абсурдный результат. В случае N = 1 соотношение (4.5) приводит к неопределенности в дисперсии типа 0/0, что более правильно отражает наше незнание величины дисперсии в случае одного измерения. При увеличении N соотношения (4.4) и (4.5) приводят практически к одинаковым результатам.
и D = 0. Т.е. получается явно абсурдный результат. В случае N = 1 соотношение (4.5) приводит к неопределенности в дисперсии типа 0/0, что более правильно отражает наше незнание величины дисперсии в случае одного измерения. При увеличении N соотношения (4.4) и (4.5) приводят практически к одинаковым результатам.
Дисперсия измерений представляет собой усредненное среднеквадратичное отклонение результатов отдельных измерений 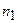 ,
, 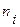 , …,
, …, 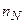 от среднего значения
от среднего значения  . При N>>1 в интервале
. При N>>1 в интервале 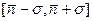 оказывается около 70% событий.
оказывается около 70% событий.
Дата добавления: 2015-05-16; просмотров: 1312;
