Распределение Пуассона
Теперь перейдем к более детальному описанию статистического распределения событий. Постараемся ответить на следующий вопрос. В результате нескольких серий идентичных измерений получено среднее число регистрируемых частиц  . Какова при этом вероятность регистрации в отдельном измерении числа регистрируемых частиц равного n? Вероятность P(n) наблюдения значения n при средней величине
. Какова при этом вероятность регистрации в отдельном измерении числа регистрируемых частиц равного n? Вероятность P(n) наблюдения значения n при средней величине  дается распределением Пуассона:
дается распределением Пуассона:
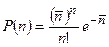 . (4.6)
. (4.6)
Распределение Пуассона - это распределение случайной величины n, принимающей целые неотрицательные значения. Оно определяет вероятность наблюдения величины n в конкретном измерении, если события происходят независимо и характеризуются средней величиной  .
.
Одним из классических примеров распределения Пуассона является распределение числа распадов радиоактивного источника постоянной интенсивности. Распределение Пуассона в этом случае описывает вероятность наблюдения различные значения числа отсчётов n вокруг среднего значения интенсивности  .
.
Выведем формулу Пуассона на примере распада радиоактивного источника состоящего из радиоактивных ядер одного изотопа. Постоянная распада - 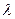 . Обозначим
. Обозначим 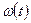 вероятность того, что ядро, достоверно существовавшее в момент t = 0, еще существует в момент t. Тогда величина
вероятность того, что ядро, достоверно существовавшее в момент t = 0, еще существует в момент t. Тогда величина 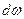 будет вероятностью распада ядра за период между t и t+dt. Очевидно, что
будет вероятностью распада ядра за период между t и t+dt. Очевидно, что
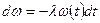 , (4.7)
, (4.7)
поскольку вероятность распада за промежуток dt равна произведению вероятности 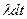 распада ядра, достоверно существующего в момент t, на вероятность
распада ядра, достоверно существующего в момент t, на вероятность 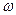 того, что ядро в момент t существует. Интегрируя (4.7) с учетом того, что
того, что ядро в момент t существует. Интегрируя (4.7) с учетом того, что 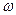 = 1 при t = 0, получим
= 1 при t = 0, получим
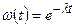 . (4.8)
. (4.8)
Соотношение (4.8) содержит полное описание статистических свойств процесса радиоактивного распада. Согласно (4.8) для одного ядра вероятность не распасться за время t равна
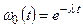 ,
,
а вероятность распасться за время t равна
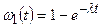 .
.
Для двух ядер, воспользовавшись независимостью их распадов, найдем, что вероятности наблюдать за время t ноль, один и два распада равны соответственно
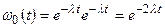 ,
,
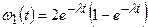 ,
,
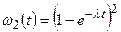 .
.
Например, для получения вероятности 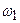 надо сначала умножить вероятность
надо сначала умножить вероятность 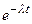 того, что первое ядро не распалось за время t, на вероятность
того, что первое ядро не распалось за время t, на вероятность 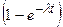 того, что второе ядро при этом распадается, а затем полученный результат удвоить, так как возможна ситуация, в которой ядра могут поменяться ролями.
того, что второе ядро при этом распадается, а затем полученный результат удвоить, так как возможна ситуация, в которой ядра могут поменяться ролями.
Аналогично для N ядер получим
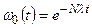 ,
,
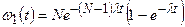 ,
,
…,
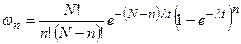 .
.
При практических измерениях, как правило, с высокой точностью справедливы приближения n<<N (число регистрируемых распадов несравненно меньше полного числа радиоактивных ядер) и 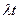 <<1 (время измерения мало по сравнению со средним временем жизни изотопа).
<<1 (время измерения мало по сравнению со средним временем жизни изотопа).
Первое из этих неравенств позволяет в выражении для 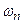 заменить N! на Nn(N-n)!, после чего с помощью второго неравенства получим распределение Пуассона:
заменить N! на Nn(N-n)!, после чего с помощью второго неравенства получим распределение Пуассона:
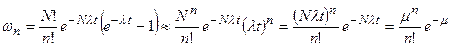 . (4.9)
. (4.9)
где введено обозначение 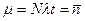 .
.
Посмотрим, как будет зависеть 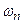 от n при обычно соблюдаемом в экспериментах условии N
от n при обычно соблюдаемом в экспериментах условии N 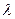 t>> 1. При малых n величина
t>> 1. При малых n величина 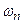 очень мала (из-за большого отрицательного показателя в экспоненте). С ростом n начнется увеличение
очень мала (из-за большого отрицательного показателя в экспоненте). С ростом n начнется увеличение 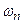 за счет множителя (N
за счет множителя (N 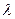 t)n. При n = N
t)n. При n = N 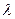 t это увеличение прекратится и сменится падением, так как знаменатель n! будет расти быстрее числителя. Таким образом,
t это увеличение прекратится и сменится падением, так как знаменатель n! будет расти быстрее числителя. Таким образом, 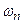 представляет собой функцию с максимумом при n = N
представляет собой функцию с максимумом при n = N 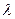 t, монотонно спадающую по обе стороны от максимума. При этом оно является асимметричным.
t, монотонно спадающую по обе стороны от максимума. При этом оно является асимметричным.
Нетрудно убедиться, что, несмотря на сделанные в (4.9) приближения, сумма всех вероятностей 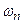 остается равной единице:
остается равной единице:
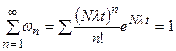 .
.
Зная выражение для вероятности 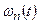 того, что за время t распадется n частиц, мы можем вычислять средние
того, что за время t распадется n частиц, мы можем вычислять средние 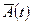 для любых зависящих от числа частиц величин
для любых зависящих от числа частиц величин 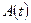 по обычной формуле для среднего:
по обычной формуле для среднего:
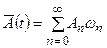 . (4.10)
. (4.10)
Так, для среднего числа ядер 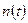 , распавшихся за время t, получим
, распавшихся за время t, получим
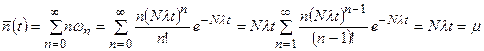 . (4.11)
. (4.11)
Таким образом, среднее число ядер, распадающихся в единицу времени, совпадает с максимумом пуассоновского распределения.
Из (4.11) видно, что активность A определяется формулой
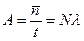 , (4.12)
, (4.12)
N - начальное число распадающихся ядер. Независимость активности от времени связана с принятым выше приближением 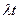 <<1.
<<1.
Для получения статистических отклонений от средних значений вычислим дисперсию D, определяемую формулой
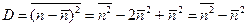 . (4.13)
. (4.13)
Величина 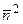 получается из (4.11):
получается из (4.11):
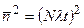 . (4.14)
. (4.14)
Величина 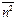 вычисляется по аналогии с (4.11):
вычисляется по аналогии с (4.11):
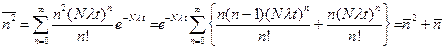 . (4.15)
. (4.15)
Отсюда для дисперсии в случае распределения Пуассона получается выражение
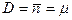 . (4.16)
. (4.16)
Стандартное отклонение
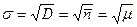 . (4.17)
. (4.17)
Итак, распределение Пуассона
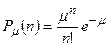
характеризуется всего одним параметром 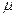 , представляющим собой среднее число отсчетов, которое мы ожидаем получить в случае многократного повторения измерений.
, представляющим собой среднее число отсчетов, которое мы ожидаем получить в случае многократного повторения измерений.
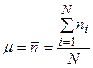 .
.
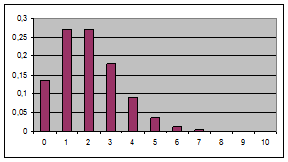
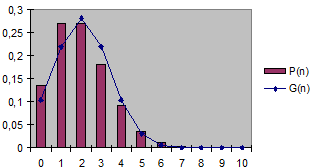
На рис. 4.2 показаны распределения Пуассона для случаев 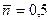 ,
, 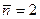 и
и 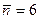 . Видно, что в случае
. Видно, что в случае 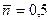 наиболее вероятные значения результатов отдельных измерений n = 0, 1. В случае
наиболее вероятные значения результатов отдельных измерений n = 0, 1. В случае 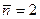 наиболее вероятны значения n = 1, 2, 3. Для малых значений
наиболее вероятны значения n = 1, 2, 3. Для малых значений  распределение Пуассона ассиметрично относительно
распределение Пуассона ассиметрично относительно 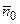 . Как видно из рис. 4.2, распределение Пуассона имеет довольно значительную ширину. Так, например, в случае
. Как видно из рис. 4.2, распределение Пуассона имеет довольно значительную ширину. Так, например, в случае 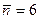 довольно большая вероятность того, что измеренное значение может быть равно от 2 до 10.
довольно большая вероятность того, что измеренное значение может быть равно от 2 до 10.
Если проведено только одно измерение, то оценкой среднего значения будет измеренное в этом эксперименте значение 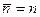 . Оценкой стандартного отклонения является величина
. Оценкой стандартного отклонения является величина 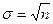 . Для ожидаемого среднего значения числа отсчётов в результате одного измерения получается следующая оценка результата измерения:
. Для ожидаемого среднего значения числа отсчётов в результате одного измерения получается следующая оценка результата измерения:
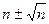 . (4.18)
. (4.18)
При n>> 1 в указанном интервале будет находиться около 70 % из общего количества зарегистрированных частиц.
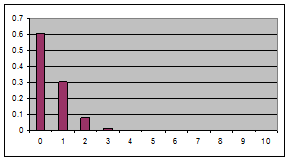
Относительная ошибка результата измерения d определяется соотношением
 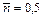
|
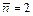
|
|
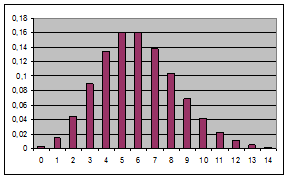
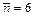 Рис. 4.2. Распределения Пуассона для случаев
Рис. 4.2. Распределения Пуассона для случаев 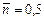 , , 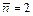 и и 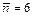 . .
|
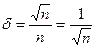 . (4.19)
. (4.19)
Если увеличить время измерения или число измерений в m раз, не изменяя другие условия эксперимента, то получится большее число отсчетов - mn, и одновременно увеличится стандартное отклонение
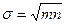 . (4.20)
. (4.20)
Однако относительная погрешность d при этом уменьшится
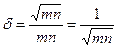 . (4.21)
. (4.21)
Рассмотрим это на примере проведенных нами измерений.
Первое измерение активности радиоактивного препарата в течение 1 секунды дало значение активности источника A = 84 отсчетов/сек. Рассчитанное стандартное отклонение
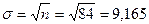 отсчетов/сек.
отсчетов/сек.
Относительная ошибка в этом случае составляет
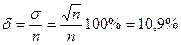 .
.
Для повышения точности измерений увеличим время эксперимента в 10 раз. Пусть за это время число отсчетов регистрирующего устройства составило n = 796. В этом случае величина стандартного отклонения для активности составила
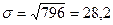 .
.
Относительная ошибка измерения уменьшилась и составила
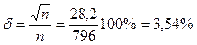 .
.
Если привести полученный результат к 1 секунде, т.е. получить значение активности источника, то
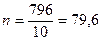 имп./сек,
имп./сек,
т.е. полученный результат будет гораздо точнее, т.к. относительная точность результата теперь равна 3,54%.
В первом случае для активности источника было получено значение
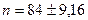 распадов/сек,
распадов/сек,
во втором -
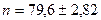 распадов/сек.
распадов/сек.
Результаты обоих измерений в пределах ошибок согласуются, но точность второго измерения выше. Чем больше распадов зарегистрировано в результате измерений, тем выше относительная точность результатов измерений.
Таким образом, если результаты отдельного измерения величины n распределены вокруг среднего значения n с шириной 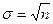 , то результат N аналогичных измерений будет распределен вокруг среднего значения
, то результат N аналогичных измерений будет распределен вокруг среднего значения  , но с шириной
, но с шириной 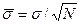 , где
, где 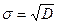 . Величина
. Величина 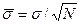 называется стандартным отклонением среднего, для серии из N независимых измерений.
называется стандартным отклонением среднего, для серии из N независимых измерений.
Корректный способ представления результата измерения состоит в том, что обычно указывают среднюю величину  и величину её стандартного отклонения
и величину её стандартного отклонения
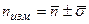 .
.
Стандартное отклонение среднего, деленное на среднее число частиц, называется относительной ошибкой измерения 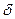 :
:
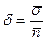 . (4.22)
. (4.22)
Нормальное распределение (распределение Гаусса)
С увеличением  распределение Пуассона становится всё более симметричным относительно
распределение Пуассона становится всё более симметричным относительно  , а относительная дискретность событий становится практически незаметной. Для больших значений
, а относительная дискретность событий становится практически незаметной. Для больших значений  , распределение Пуассона переходит в распределение Гаусса
, распределение Пуассона переходит в распределение Гаусса
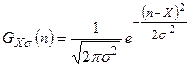 . (4.23)
. (4.23)
Функция 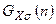 называется также функцией Гаусса. Говорят, что результаты измерений имеют нормальное распределение, если они описываются функцией Гаусса.
называется также функцией Гаусса. Говорят, что результаты измерений имеют нормальное распределение, если они описываются функцией Гаусса.
Распределение Гаусса является симметричным, непрерывным и, в отличие от распределения Пуассона, характеризуется двумя независимыми параметрами Х и 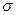 . X - среднее число отсчетов, которое мы ожидаем получить в случае многократного повторения измерений.
. X - среднее число отсчетов, которое мы ожидаем получить в случае многократного повторения измерений. 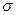 - среднее стандартное отклонение (на интервал [X-
- среднее стандартное отклонение (на интервал [X- 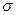 , X+
, X+ 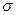 ] в среднем приходится 68%, а интервал [X-2
] в среднем приходится 68%, а интервал [X-2 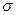 , X+2
, X+2 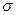 ] - 95% всех регистрируемых событий).
] - 95% всех регистрируемых событий).
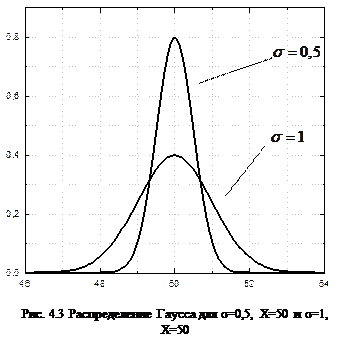 Оказывается, что если на результаты измерений оказывают влияние большое число источников небольших случайных ошибок, то вся совокупность измерений имеет в качестве предельного распределения симметричную колоколообразную функцию Гаусса. Центр распределения X, совпадающий с его максимумом, будет истинным значением измеряемой величины.
Оказывается, что если на результаты измерений оказывают влияние большое число источников небольших случайных ошибок, то вся совокупность измерений имеет в качестве предельного распределения симметричную колоколообразную функцию Гаусса. Центр распределения X, совпадающий с его максимумом, будет истинным значением измеряемой величины.
Распределение Гаусса (4.23) нормировано на единицу.
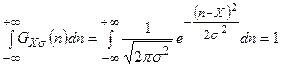 .На рис. 4.3 показано два нормальных или гауссовых распределения, соответствующие различным измерениям с одинаковыми значениями X и разными s. В первом случае Х=50,
.На рис. 4.3 показано два нормальных или гауссовых распределения, соответствующие различным измерениям с одинаковыми значениями X и разными s. В первом случае Х=50, 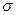 =0,5, во втором случае - Х=50,
=0,5, во втором случае - Х=50, 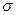 =1. Величина
=1. Величина 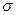 в знаменателе экспоненты обеспечивает для более узкого распределения большую высоту в максимуме.
в знаменателе экспоненты обеспечивает для более узкого распределения большую высоту в максимуме.
В случае распределения Гаусса ожидаемое среднее значение  для большого числа измерений можно вычислить по стандартной формуле
для большого числа измерений можно вычислить по стандартной формуле
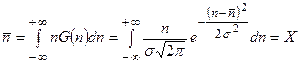 . (4.24)
. (4.24)
Этот результат почти очевиден, т. к. при большом числе измерений вследствие симметрии функции Гаусса одинаковое число результатов измерений окажется как больше X, так и меньше X. Среднее стандартное отклонение 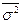 определяется соотношением
определяется соотношением
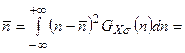
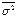 . (4.25)
. (4.25)
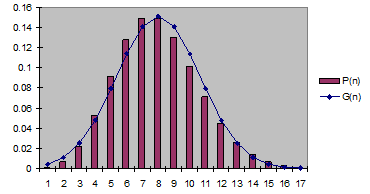
Сравним распределения Гаусса 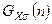 и Пуассона
и Пуассона 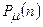 .
.
|
|
|

|
| Рис. 4.4. Сравнение распределений Пуассона и Гаусса |
1. Распределение Гаусса 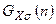 является непрерывным, т.к. величина n может быть непрерывной, в то время как в распределении Пуассона
является непрерывным, т.к. величина n может быть непрерывной, в то время как в распределении Пуассона 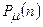 величина n = 0, 1, 2, 3, … дискретна.
величина n = 0, 1, 2, 3, … дискретна.
2. Распределение Гаусса определяется двумя параметрами: X - средней величиной и шириной распределения - стандартным отклонением 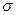 , в то время как распределение Пуассона определяется единственным параметром
, в то время как распределение Пуассона определяется единственным параметром 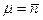 , т.к. ширина распределения Пуассона
, т.к. ширина распределения Пуассона 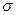 автоматически определяется величиной
автоматически определяется величиной 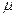 (
( 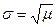 ).
).
3. При увеличении среднего числа отсчетов дискретная природа величины 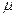 в распределении Пуассона становится менее существенна, и распределение Пуассона хорошо аппроксимируется функцией Гаусса:
в распределении Пуассона становится менее существенна, и распределение Пуассона хорошо аппроксимируется функцией Гаусса:
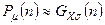 ,
,
при 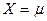 ,
, 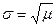 .
.
На рис. 4.4 сравниваются распределение Пуассона и распределение Гаусса для двух значений 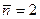 и
и 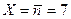 .
. 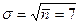 . Видно, что уже при достаточно малых значениях
. Видно, что уже при достаточно малых значениях 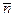 распределения Пуассона и Гаусса практически совпадают. Необходимо иметь в виду, что распределения Пуассона и Гаусса совпадают только тогда, когда для распределения Гаусса
распределения Пуассона и Гаусса практически совпадают. Необходимо иметь в виду, что распределения Пуассона и Гаусса совпадают только тогда, когда для распределения Гаусса 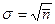 . В общем случае распределение Гаусса характеризуется двумя независимыми параметрами
. В общем случае распределение Гаусса характеризуется двумя независимыми параметрами 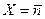
 и
и 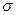 . Величина
. Величина 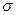 может быть как больше
может быть как больше 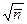 , так и меньше.
, так и меньше.
В качестве примера распределения Гаусса укажем измерение энергетических спектров частиц. При измерении энергетических спектров заряженных частиц на выходе усилителя спектрометра мы имеем сигналы, амплитуда которых несет информацию об их энергиях. За счет различных процессов, носящих случайный характер (шумы детектора, флуктуации зарядового состояния ионов и т.п.), амплитуды сигналов от монохроматического источника имеют гауссово распределение, которое определяется двумя параметрами средним значением амплитуды сигнала Х и среднеквадратичным отклонением 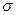 . Разрешение спектрометра – это полная ширина на половине высоты (Full Width at Half Maximum - FWHM). В данном случае величины Х и
. Разрешение спектрометра – это полная ширина на половине высоты (Full Width at Half Maximum - FWHM). В данном случае величины Х и 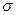 в отличие от распределения Пуассона независимы
в отличие от распределения Пуассона независимы
Дата добавления: 2015-05-16; просмотров: 1774;
