Глава 7. Элементы математической статистики

Основные понятия и основные задачи математической статистики

В математической статистике исследуются способы получения выводов на основе эмпирических (опытных) данных. Основными понятиями математической статистики являются: генеральная совокупность, выборка, теоретическая функция распределения.

Определение. Генеральной совокупностью называются все возможные результаты наблюдений, которые могут быть сделаны при данном комплексе условий.

В некоторых задачах генеральную совокупность рассматривают как случайную величину 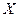. Примером генеральной совокупности может быть все население страны. В этой совокупности нас могут интересовать, например, возраст жителей. Другим примером генеральной совокупности являются детали, изготовленные на данном станке. Эти детали могут быть качественными и бракованными.

Определение. Выборочной совокупностью (выборкой) называется множество результатов, случайно отобранных из генеральной совокупности.

Выборка должна быть репрезентативной, т.е. правильно отражать пропорции генеральной совокупности. Это достигается случайностью отбора, когда все объекты генеральной совокупности имеют одинаковую вероятность быть отобранными.

Определение. Число объектов в совокупности (генеральной или выборочной) называется ее объемом.

Объем генеральной совокупности обозначим символом 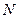, а объем выборочной совокупности обозначим символом 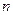. При этом подразумевается, что .

Заметим, что сам процесс выбора можно осуществлять разными способами: выбрав объект и определив его значение, изымать объект и не допускать к последующим испытаниям (выборка без возвращения); после определения его значения объект возвращается в генеральную совокупность (выборка с возвращением). Очевидно, что при достаточно большом объеме генеральной совокупности исчезает различие между выборками с возвращением и без возвращения. Будем рассматривать случай бесконечно большого объема генеральной совокупности.

Основные задачи математической статистики:

1. Оценка значения неизвестной вероятности случайного события;

2. Определение неизвестной теоретической функции распределения;

3. Определение неизвестных параметров распределения теоретической функции распределения;

4. Проверка статистических гипотез;

5. Оценка зависимости.