Задание для выполнения расчетно-графической работы № 5.
Для вариантов 1; 2; 11; 12; 21; 22; 31; 32.
Для двухопорной балки, нагруженной равномерно распределенной нагрузкой интенсивностью q , силой F и парой сил с моментом М, определить реакции опор, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный изгибающий момент и из условия прочности определить размеры поперечного сечения «b» и «h» деревянной балки прямоугольного поперечного сечения, если h = 2b , [s ] = 10 МПа
Для вариантов 3-30 ( кроме указанных выше).
Для двухопорной балки, нагруженной равномерно распределенной нагрузкой интенсивностью q , силой F и парой сил с моментом М, определить реакции опор, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный изгибающий момент и из условия прочности подобрать сечение балки в виде двутавра. Материал – сталь [sр ] = [sс ] = 160 МПа.
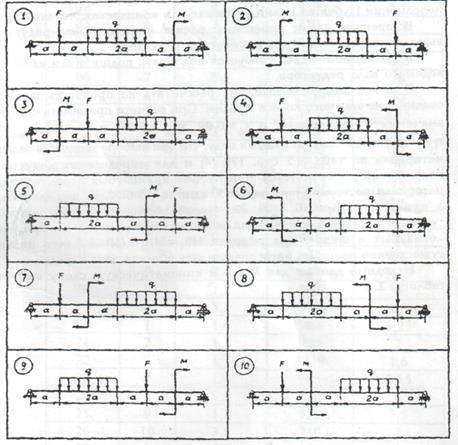
| № Задания | ||||||||||
| F, кН | ||||||||||
| М , к Н м | ||||||||||
| q, к Н/м | ||||||||||
| a, м | 0,2 | 0,2 | 0,3 | 0,3 | 0,4 | 0,4 | 0,5 | 0,5 | 0,6 | 0,6 |
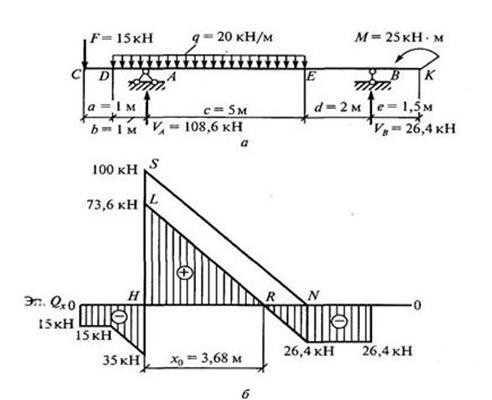
Пример 1.Построить эпюры поперечных сил и изгибающих моментов, подобрать № профиля стальной двутавровой балки.
|
|
|
|
|
|
|
|
Решение:
1. Определим опорные реакции балки. Составим уравнения:
1) åMA = 0; 2) åMB = 0.
Из первого уравнения найдем VB:
-F(a + b) + q(b + c)((b + c)/2 - b)) - RBY(c + d) - M = 0
или
-15 × 2 + 20 × 6 × 2 - RBY × 7 - 25 = 0,
откуда
VB= (-15 × 2 + 20 × 6 × 2 - 27) / 7 = 26,4 кН.
Из второго уравнения найдем VA :
-F(a + b + c + d) + RAY(c + d) - q(b + c)((b + c)/2 + d)) - M = 0
или
-15 × 9 + RAY × 7 - 20 × 6 × 5 - 25 = 0,
откуда
VA= (15 × 9 + 20 × 6 × 5 + 25) / 7 = 108,6 кН.
Выполним проверку:
åY = RAY + RBY - F - q(b + c) = 0
или
108,6 + 26,4 - 15 - 20 × 6 = 0, откуда 135 - 135 = 0.
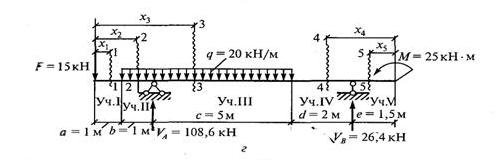
2. Обозначим характерные сечения балки C, D, A, E, B, K.
3. Построение эпюры Q:
Участок 1.
Q1 = -F; 0 м £ Z1 £ 1 м;
Z1 = 0 м; Q1 = -15 кН;
Z1 = 1 м; Q1 = -15 кН;
Участок 2.
Q2 = -F - q(Z2 - 1); 1 м £ Z2 £ 2 м;
Z2 = 1 м; Q2 = -15 - 20(1 - 1) = -15 кН;
Z2 = 2 м; Q2 = -15 - 20(2 - 1) = -35 кН;
Участок 3.
Q3 = -F - q(X3 - 1) + RAY; 2 м £ Z3 £ 7 м;
Z3 = 2 м; Q3 = 73,6 кН;
Z3 = 7 м; Q3 = -15 - 20(7 - 1) + 108,6 = -26,4 кН;
Участок 4.
Q4 = -RBY; 1,5 м £ Z4 £ 3,5 м;
Z4 = 1,5 м; Q4 = -26,4 кН;
Z4 = 3,5 м; Q4 = -26,4 кН;
Участок 5. Сечение от правого конца балки.
Q5 = 0; 0 м £ Z5 £ 1,5 м;
Z5 = 0 м; Q5 = 0 кН;
Z5 = 1,5 м; Q5 = 0 кН;
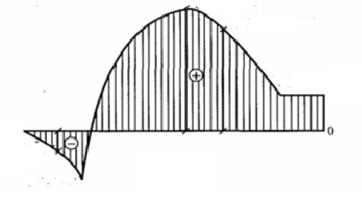
4. Построение эпюры MZ:
Участок 1.
MZ1 = -F × X; 0 м £ Z1 £ 1 м;
Z1 = 0 м; MZ1 = 0 кН;
Z1 = 1 м; MZ1 = -15 × 1 = -15 кН;
Участок 2.
MZ2 = -F × Z2 - q(Z2 - 1)2 / 2; 1 м £ Z2 £ 2 м;
Z2 = 1 м; MZ2 = -15 × 1 - 20 × (1 - 1)2 / 2 = -15 кН×м;
Z2 = 2 м; MZ2 = -15 × 1 - 20 × (2 - 1)2 / 2 = -40 кН×м;
Эпюра Q на этом участке не пересекает нулевую линию, то есть эпюра на этом участке не будет иметь экстремума и ее можно построить по двум точкам.
Участок 3.
MZ3 = -F × Z3 - q(Z3 - 1)2 / 2 + RAY(Z3 - 2); 2 м £ Z3 £ 7 м;
Эпюра представляет собой параболу.
Z3 = 2 м; MZ3 = -15 × 2 - 20 × (2 - 1)2 / 2 + 108,6 × (2 - 2) = -40 кН×м;
Z3 = 7 м; MZ3 = -15 × 7 - 20 × (7 - 1)2 / 2 + 108,6 × (7 - 2) = -78 кН×м;
На этом участке эпюра имеет экстремум: для определения приравняем первую производную закона изменения MZ нулю, то есть:
dMZ3 / d3 Z3 = 0;
-F - 2q(Z3 - 1) / 2 + RAY = 0;
или
-F - q(Z3 - 1) + RAY = 0;
-15 - 20 × (Z3 - 1) + 108,6 = 0;
Z3 = (-15 + 20 + 108,6) / 20 = 5,68 м.
От опоры А 5,68 - 2 = 3,68 м.
Изгибающий момент в этом сечении:
MZ3 = -15 × 5,68 - 20 × (5,68 - 1)2 / 2 + 108,6 × (5,68 - 2) = 95,4 кН×м.
Участок 4.
MZ4 = M + RBY ( Z4 - 1,5); 1,5 м £ Z4 £ 3,5 м;
Z4 = 1,5 м; MZ4 = 25 - 26,4 × (1,5 - 1,5) = 25 кН×м;
Z4 = 3,5 м; MZ4 = 25 +26,4 × (3,5 - 1,5) = 78 кН×м;
Участок 5.
MZ5 = M; 0 м £ Z5 £ 1,5 м;
Z5 = 0 м; MZ5 = 25 кН×м;
Z5 = 1,5 м; MZ5 = 25 кН×м;
Строим эпюру MZ.
5. Подобрать № профиля балки из стального двутавра
[s] = 160 МН / м2.
5.1 По эпюре изгибающих моментов находим Mmax = 0,54 кН×м.
5.2 Требуемый момент сопротивления поперечного сечения балки из условия прочности
Wmax ³ Mmax / [s] = (95,4 × 103) / (160 × 106) = 596,25 × 10-6 м3 = 596,25 см3
По таблицам ГОСТ 8240-72 принимаем двутавр №33.
Дата добавления: 2015-05-28; просмотров: 3626;
