II. Методика работы. Одним из наиболее распространенных приборов для получения спектров является дифракционная решетка

Одним из наиболее распространенных приборов для получения спектров является дифракционная решетка. Простейшая оптическая дифракционная решетка представляет собой стеклянную пластинку, на которой с помощью делительной машины нанесен ряд параллельных штрихов. Штрихи служат непрозрачными промежутками, разделяющими прозрачные участки, называемые щелями. У дифракционной решетки все щели имеют одинаковую ширину а , непрозрачные промежутки между ними – ширину в. Сумму а + в = d называют периодом или постоянной решетки. В зависимости от положения точки наблюдения (здесь угла φ), в щели а может укладываться четное либо нечетное количество зон Френеля; тогда в этой точке после прохождения света через щель будет наблюдаться соответственно дифракционный минимум или максимум. Если число зон равно 2k – четное, то такие углы наблюдения определяют условие главных минимумов дифракционной решетки:

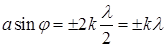. (10.1)

Однако, определяющим принципом в работе дифракционной решетки является не дифракция на щели а, но интерференция многих пучков, идущих через отверстия, расположенные на расстояниях, кратных d – периоду решетки. Схематическое изображение хода двух соседних лучей при прохождении через дифракционную решетку дано на рис. 10.3.

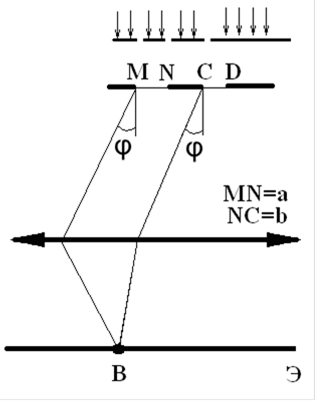
Рис.10.3. Схема интерференции от двух соседних лучей.

Разность хода для любых двух соседних лучей, наблюдаемых под углом φ, равна:

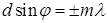, (10.2)

что является условием наблюдения главных максимумов дифракционной решетки. Интерференция от соседних лучей дает также дополнительные минимумы:

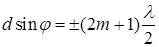. (10.3)

Если на дифракционную решетку будет падать немонохроматический свет, то дифракционные максимумы для волн разного цвета так же, как и при дифракции от одной щели, пространственно разойдутся. Центральные максимумы (m = 0, φ = 0) для всех длин волн совпадут, но уже максимумы первого порядка (m = 1) будут для фиолетовых лучей расположены ближе к центру, чем для красных. Из уравнения (10.2) видно, что синусы углов в спектре данного порядка прямо пропорциональны длинам волн:

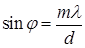. (10.4)

Зная углы φ_i , под которыми видны данные линии спектра, можно найти их длины волн; расчетная формула для нахождения λ_i:

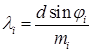. (10.5)

Основными характеристиками дифракционной решетки являются её разрешающая способность и дисперсия.

Разрешающая способность — это возможность разделять две спектральные линии, мало отличающиеся друг от друга по длине волны, т.е. видеть их в спектре как две линии, а не как одну. Разрешающей способностью любого спектрального прибора называется отношение длины той волны, около которой производится измерение, к наименьшему интервалу длин волн, который может быть обнаружен и измерен этим прибором.

Расчет показывает, что разрешающая способность R дифракционной решетки

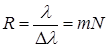, (10.6)

где N – общее число штрихов решетки; m – наибольший порядок спектра.

В решетке большая разрешающая способность достигается за счет больших значений N, так как порядок m обычно не велик.

Чем больше число щелей N, тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется между соседними главными максимумами, тем, следовательно, более интесивными и более острыми (четкими) будут главные максимумы.