II. Методика работы.

Свет от первичного источника S (рис. 9.2) падает на диафрагму D , имеющую два маленьких отверстия. По принципу Гюй­генса эти отверстия служат вторичными когерентными источниками света S₁ и S₂ и дают на экране картину интерференции.

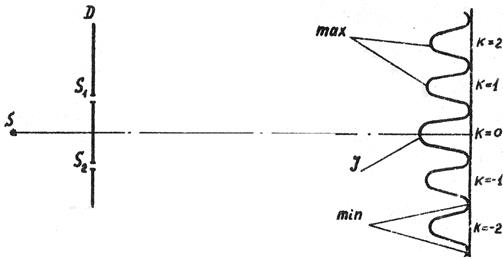
Рис. 9.2. Картина интерференции от двух источников.

Для нахождения положений max и min интерференции необходимо рассчитать разность хода Δ (см. (V.2)).

Для вывода расчетной формулы обратимся к рис 9.3, из которого видно, что разность хода в данном случае равна разности геометрических длин пути r₂ и r₁ для лучей, т.к. показатель преломления для воздуха :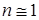

Δ = Δ_r = r₂ – r₁ . (9.1)

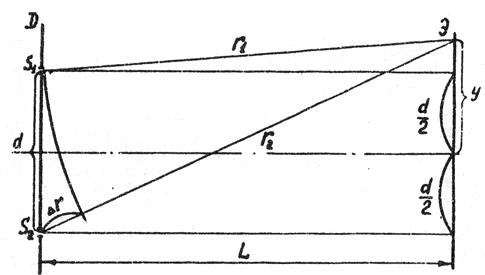
Рис. 9.3. Схема хода лучей при интерференции по методу Юнга

Используя теорему Пифагора, найдем:

r₂² = L² – (y + d/2)², r₁² = L² – (y – d/2)². (9.2)

Вычитая r₁² из r₂² , получаем:

(r₂ – r₁) ∙ (r₂ – r₁) = 2∙y∙d . (9.3)

Но из условий опыта следует, что ордината y максимумов и минимумов интерференции приблизительно на порядок меньше расстояния до экрана L. Следовательно, r₂ + r₁ ≈ 2∙L и

Δ = r₂ – r₁ = 2∙y∙d/(2∙L) = y∙d/L (9.4)

Итак, с учетом формул (9.1), (9.2) и (9.4) мы можем окончательно записать формулы, дающие ординаты максимумов

y_max = ±k∙λ∙(L/d) (9.5 а)

и минимумов

y_min = ±(2∙k + 1) ∙ (λ/2) ∙ (L/d) (9.5 б)

Максимум, которому соответствует k=0, называется максимумом нулевого порядка; максимумы, которым соответствует k = 1, 2, 3, … называют максимумами 1, 2, 3, … и т.д. порядков (см. рис. 92).

Расстояние между серединами ближайших max или min называют шириной полосы t ~ λ и, в случае сложного света, это ведет к разложению белого света при интерференции. В нашем опыте свет от лазера монохроматический.

Ширину полосы найдем, вычитая в (9.5 а или б) значения y_k и y_k-1 :

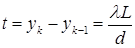. (9.6)

Тогда расчетная формула для определения длины волны:

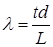. (9.7)