Задачи для самостоятельного решения. Задача 1.Определить моменты шести заданных сил относительно точек А, Ви С, если F1 = 30 Н, F2 = 50 Н

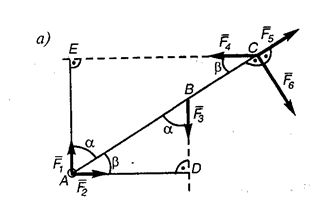
Задача 1.Определить моменты шести заданных сил относительно точек А, Ви С, если F₁ = 30 Н, F₂ = 50 Н, F₃ = 25 Н, F₄ = 40 Н, F₅ = 35 Н, F₆ = 54 Н, АВ = 1,2 м, ВС = 0,8 м, a = 55° и b = 35°.

Вопросы для самопроверки

1. Чем оценивается действие пары сил на тело?

2. Как называется расстояние между линиями действия сил пары?

3. Как можно сложить пары сил?

4. Что называется плоскостью действия пары?

5. Чему равен момент равнодействующей пары?

2.3 Тема: Плоская система произвольно расположенных сил. Определение реакций опор и моментов защемления.

Иметь представление о видах опор и возникающих реакциях в опорах.

Знать три формы уравнений равновесия и уметь их использовать для определения реакций в опорах балочных систем.

Уметь выполнять проверку правильности решения.

Практическое занятие проводится после изучения темы «Плоская система произвольно расположенных сил».

По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если передача нагрузки происходит на малой площадке( в точке), нагрузку называют сосредоточенной. Если нагрузка распределена на значительной площадке или линии (давление воды на плотину, давление снега на крышу и т.п), нагрузку считают распределенной.

В задачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой:

G = q ·l

q - интенсивность нагрузки;

l - длина интенсивности;

Балка – конструктивная деталь в виде прямого бруса, закрепленная на опорах и изгибаемая приложенными к ней силами.

Жесткая заделка (защемление).Опора не допускает перемещений и поворотов. Заделку заменяют двумя составляющими силы R_AX и R_AY и парой с моментом M_R. Для определения этих неизвестных используют систему уравнений:

ΣX = 0

ΣY = 0

ΣMA = 0

Для проверки правильности решения используют дополнительное уравнение моментов относительно любой точки на балке:

ΣМ_В = 0

Балка на двух шарнирных опорах.Неизвестны три силы. В этом случае удобно использовать систему уравнений во второй форме:

ΣМ_А = 0

ΣМ_В = 0

ΣХ = 0

Для контроля правильности решения используют уравнение:

ΣY = 0.