Последовательность решения.
1. Изобразить балку вместе с нагрузками.
2. Выбрать расположение координатных осей, совместив ось X с балкой, а ось Y направив перпендикулярно оси Х.
3. Произвести необходимые преобразования заданных активных сил: силу наклоненную к оси балки под углом a заменить двумя взаимно перпендикулярными составляющими, а равномерно распределенную нагрузку заменить ее равнодействующей, приложенной в середине участка распределения нагрузки.
4. Освободить балку от опор, заменив их действие реакциями опор, направленных вдоль выбранных осей координат.
5. Составить уравнение равновесия для произвольной плоской системы сил.
6.
|
|





 Проверить правильность найденных опорных реакций по уравнению, которое не было использовано для решения задач. То есть составить уравнение åY = 0.
Проверить правильность найденных опорных реакций по уравнению, которое не было использовано для решения задач. То есть составить уравнение åY = 0.
q1 = 20 кН/м

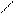









|
|







 q2 = 15 кН/м
q2 = 15 кН/м
|
|
|


 М = 25 кН×м
М = 25 кН×м
|
|
|







 F = 30 кН
F = 30 кН
|
|







Решение:
1. Обозначим опоры А и В.
2. Укажем опорные реакции
Ray; Rby; Rax;
3. Определим равнодействующие равномерно распределенной нагрузки
Q1 = q1 × (a + b) = 20 × 4,5 = 90 кН
Q2 = q2 × (2× d) = 15 × 3 = 45 кН
4. Составим уравнение равновесия
 åМА = 0 Q1×((a +b)/2- a) - F×(b + c) +Q2×(b + c + d) - Rby×(b+ c+ d) - M = 0
åМА = 0 Q1×((a +b)/2- a) - F×(b + c) +Q2×(b + c + d) - Rby×(b+ c+ d) - M = 0
åМB = 0 Ray×((b + c + d) - Q1×((a + b)/2 + c + d) + F × d - M = 0
åX = 0 Rax = 0
откуда
Rby = (Q1× ((a + b)/2 - a) - F×(b + c) + Q2×(b + c + d) - M) / (b + c + d) =
= (90 ×(4,5/2 - 1) - 30 ×(3,5 +1) + 45 × 6 - 25) / 6 = 37,1 кН
Ray = (Q2× ((a + b)/2 + c + d) - F× d + M) / (b + c + d) =
= (45 ×(4,5/2 + 1 + 1,5) - 30 × 1,5 + 25) / 6 = 67,9 кН
5. Выполним проверку, используя уравнение åY = 0.
åY = 0 | Ray - Q1 + F + Rby - Q2 = 0
67,9 - 90 + 30 + 37,1 - 45 = 0
135 - 135 = 0
Реакции определены верно.
Ответ: Ray = 67,9 кН; Rby = 37,1 кН;
Дата добавления: 2015-05-28; просмотров: 2214;
