Условия равновесия в изолированной однородной системе

Рассмотрим изолированную систему, которая состоит из двух подсистем 1 и2, и выясним условия, при которых между этими подсистемами будет равновесное состояние. В качестве критерия равновесия возьмем условие

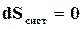. (16.56)

Поскольку энтропия является аддитивной величиной, то применительно к нашему случаю

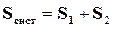, (16.57)

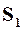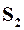где и – энтропия соответственно 1-й и 2-й подсистем.

В соответствии с равенством (16.56)

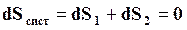. (16.58)

Из термодинамического тождества (16.20) имеем

.

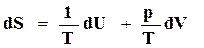Следовательно, для 1-й подсистемы можно записать

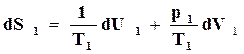, (16.59)

а для 2-й

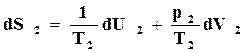. (16.60)

Подставив значения 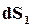и 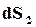из выражений (16.59) и (16.60) в уравнение (16.58), найдем

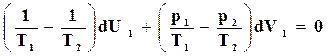. (16.61)

Внутренняя энергия U и объем Vмогут быть независимы друг от друга, причем для рассматриваемой системы

,

.

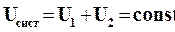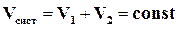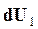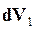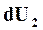Если внутренняя энергия и объем системы независимы друг от друга, следовательно, для подсистем дифференциалы и , и 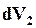также независимы.

Тогда для того чтобы левая часть уравнения (16.61) была тождественно равна нулю, нужно чтобы порознь множители при дифференциалах 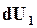и 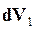также были равны нулю, т. е.

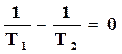, (16.62)

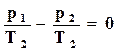. (16.63)

Из выражения (16.62) следует, что

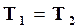, (16.64)

а из выражения (16.63) с учетом (16.64) получаем

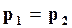. (16.65)

Таким образом, в изолированной системе в состоянии равновесия температура и давление во всех частях системы одинаковы.