Закон Гесса
Первое начало термодинамики позволяет получить закон Гесса (или закон постоянства тепловых сумм), который указывает, что теплота реакции не зависит от пути реакции, а определяется лишь начальным и конечным состояниями реагирующих веществ.
Действительно, при (T,V) = const
,
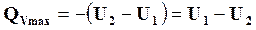т.е. количество теплоты реакции не зависит от пути перехода системы из первого состояния во второе.
Если же реакция происходит при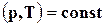 
, то
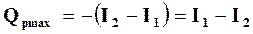
также не зависит от пути и является функцией состояния системы.
Закон Гесса позволяет вычислить теплоты таких реакций, для которых они непосредственно не могут быть измерены. В таких случаях составляют термохимические уравнения, решая которые определяют теплоту искомой реакции.
Например, при сгорании твердого углерода, который никогда не сгорает целиком в окись углерода, а всегда образует некоторое количество двуокиси СО2
, 
.
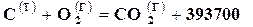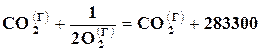Вычитая из первого уравнения второе, получим
,
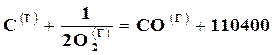т. е. при неполном сгорании углерода выделяется 110400,0 кДжна 1 моль СО, в то время как при полном сгорании углерода выделяется 393720 кДж/моль, а при сгорании окиси углерода выделяется 283300 кДж/моль СО2.
16.4Закон Кирхгофа
Характер температурной зависимости теплоты реакции определяется уравнением Кирхгофа, которое легко получить на основании первого закона термодинамики. Для этого продифференцируем по температуре выражение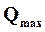 
, определяемое первым законом термодинамики.
Для реакции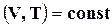 
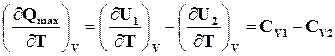, (16.12)
где СV1и СV2 – суммарные изохорные теплоемкости исходных и полученных веществ.
При изобарно-изотермических процессах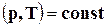 
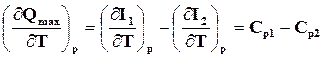(16.13)
где Ср1 и Ср2– суммарные теплоемкости при постоянном давлении исходных и полученных веществ.
Суммарные теплоемкости системы перед реакцией и после реакции могут быть подсчитаны по формулам
, 
,
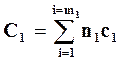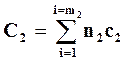где n1 иc1 – числа молей и теплоемкости исходных веществ; n2 и с2 ─ числа молей и теплоемкости полученных веществ; m1 и m2 – число компонентов исходных и полученных в реакции веществ.
Обобщение формул (16.12) и (16.13) приводит к зависимости
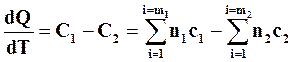. (16.14)
Полученное выражение представляет собой математическое выражение закона Кирхгофа, по которому температурный коэффициент теплоты реакции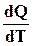 
равен разности сумм теплоемкостей исходных и полученных в реакции веществ.
Для определения теплоты реакции при любой температуре нужно знать зависимость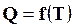 
.
Если допустить, что истинные теплоемкости определяются эмпирическим степенным рядом
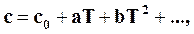
то, подставляя их значения в формулу (16.14), получим, пропустив пределы у сумм
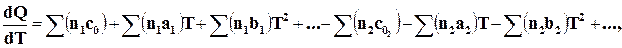
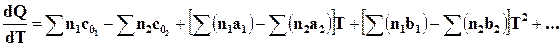, (16.15)
Интегрируя это уравнение, найдем
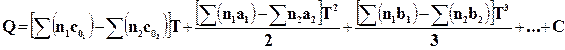, (16.16)
где С─ константа интегрирования.
Введем для сокращения записи следующие обозначения:
,
,
.
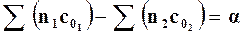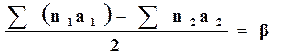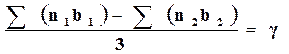Подставляя эти обозначения в (16.16), находим
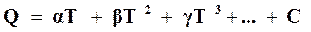. (16.17)
При Т = 0 К и С = Q0 уравнение теплоты реакции примет вид
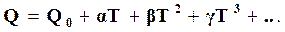(16.18)
Постоянный член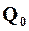 
не представляет собой теплоту реакции при абсолютном нуле, так как использованные для составления уравнения (16.18) эмпирические уравнения теплоемкости не применимы при низких температурах. Таким образом, 
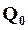– просто свободный член эмпирического уравнения, применяемого лишь в области, далекой от абсолютного нуля. Значение 
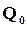может быть определено по известной теплоте реакции для какой-либо температуры.
16.5 Второй закон термодинамики и его применение к химическим процессам
В общем, виде аналитическое выражения 2-го закона термодинамики для любой изолированной системы записывалось в виде уравнения
,
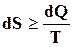где знак равенства характеризует обратимые, а знак неравенства необратимые процессы. Так как для адиабатически изолированной системы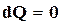 
, это неравенство принимает вид 
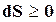, откуда следует, что энтропия такой системы может только возрастать или оставаться постоянной. В состоянии 
; 
; 
.
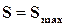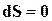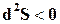Таким образом, энтропия является наиболее общей функцией, с помощью которой можно определять направление процессов и найти условия их равновесия.
Первый и второй закон термодинамики с учетом знаков, принятых в термохимии (убыль внутренней энергии положительна, а теплота, сообщенная системе, отрицательна), можно записать в следующем виде:
,
.
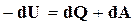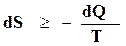Объединяя эти уравнения, получим
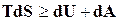. (16.19)
При отсутствии работ против немеханических сил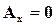 
,
.
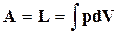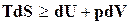, (16.20)
или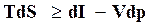 
. (16.21)
Преобразуем уравнение (16.20)
,
,
,
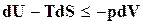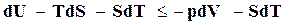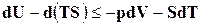Откуда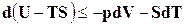 
. (16.22)
Функция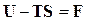 
является некоторой функцией состояния. Ее называют изохорно-изотермическим потенциалом.
С учетом выше изложенного уравнение (16.21) можно записать в виде
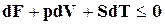. (18.23)
Знак равенства относится к обратным процессам, а неравенства – к необратимым.
Для изохорно-изотермического процесса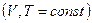 
, 
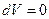и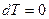 
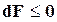. (16.24)
Следовательно, в изолированных системах, находящихся при постоянной температуре и объеме, самопроизвольно могут протекать только те процессы, которые идут с уменьшением F, причем пределом их протекания (условием равновесия) является достижение минимального, для определенных условий, значения функции F, т.е.
; 
; 
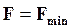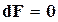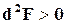. (16.25)
Рассматривая F как функцию независимых параметров Т и V, полный дифференциал ее представим в виде
.
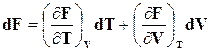Сопоставление этого выражения с уравнением (16.23) приводит к выводу, что
, 
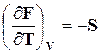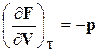. (16.26)
Соотношения (16.26) показывают, что изменение изохорно-изотермического потенциала по температуре при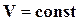 
определяется энтропией, а изменение его по объему при постоянной температуре определяется давлением.
Следовательно, Fпредставляет характеристическую функцию, так как частные производные ее позволяют выразить термодинамические свойства системы.
Подставляя значение энтропии из уравнения (16.26) в выражение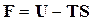 
, получим связь между изохорно-изотермическим потенциалом и внутренней энергией
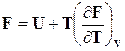. (16.27)
Если в уравнении (18.20) прибавить к обеим частям выражение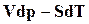 
, то после преобразования получим:
,
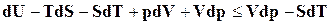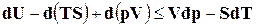, откуда
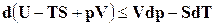. (16.28)
Обозначим
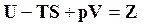. (16.29)
Так как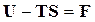 
,
то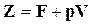 
или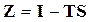 
вследствие того, что 
.
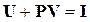Величина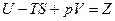 
является некоторой функцией состояния и называется изобарно-изотермическим потенциалом.
Тогда согласно уравнению (16.28)
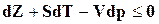. (16.30)
Для изобарно-изотермических процессов, в которых dTи dpравны нулю,
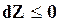. (16.31)
Следовательно, в изолированной системе при постоянном давлении и температуре самопроизвольно могут протекать только такие процессы, которые идут с уменьшением Z, причем пределом их протекания (условием равновесия) служит достижение некоторого минимального для данных условий значения функции Z, т. е.
; 
; 
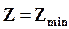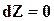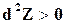. 16.32)
Как следует из уравнения (16.29), функция Z является характеристикой при независимых параметрах р и Т, при этом
,
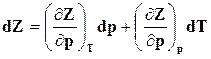последнее уравнение и (16.29) тождественны, а поэтому имеем
, 
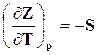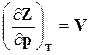. (16.33)
Если поставить найденное значение энтропии в выражение изобарно-изотермического потенциала, то получим связь между этим потенциалом и энтальпией
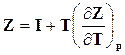. (16.34)
Таким образом, кроме такого критерия равновесия системы, как энтропия (которая принимает при равновесии максимальное значение), в частых случаях можно пользоваться величинами изохорно - и изобарно-изотермических потенциалов. Условием равновесия процессов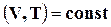 
и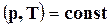 
является минимум этих потенциалов. Обе эти функции F иZ характеризуют часть внутренней энергии или энтальпии системы, которая может переходить в полезную работу.
Определим значения изохорно – и изобарно-изотермических потенциалов для идеального газа. Из термодинамического тождества (16.20), (16.21), учитывая, что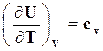 
, а 
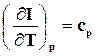, следует
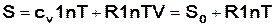, (16.35)
или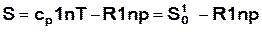 
. (16.36)
Эти уравнения выражают зависимость энтропии одного моля идеального газа от объема и давления, причем S0и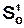 
представляет собой сумму членов, которые при постоянной температуре сохраняют постоянное значение. Вводя значение энтропии из выражений (16.35) и (16.36) в формулы 
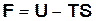и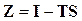 
, получим
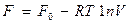, (16.37)
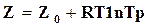, (16.38)
где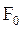 
и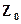 
– суммы членов, не изменяющихся при постоянной температуре.
Численно значения S0 и 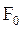соответствуют энтропии и изохорно-изотермическому потенциалу 1 моль при 
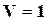, а 
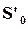и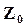 
– энтропии и изобарно-изотермическому потенциалу 1 моль при р=1,0133 бар.
Дата добавления: 2015-04-05; просмотров: 888;