Задача 2.26.
Производится три независимых испытаний приборов, в каждом из которых неисправность (событие А) появляется с вероятностью 0.4. Рассматривается случайная величина Х –– число выявленных неисправностей в трех опытах.
Необходимо построить ряд распределения и функцию распределения случайной величины Х. Найти ее математическое ожидание M[X], дисперсию D[X], среднее квадратическое отклонение sх и третий центральный момент m3[X].
Решение.
Введем обозначения:
xi –– число неисправностей, обнаруженных в трех испытаниях;
pi –– вероятность того, что в результате трех испытаний будет обнаружено ровно xi неисправностей.
Эта вероятность рассчитывается по формуле (2.33) биномиального закона распределения дискретных случайных величин. Тогда ряд распределения дискретной случайной величины и функция распределения имеют вид:
| xi | ||||
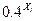
| 0.4 | 0.16 | 0.064 | |
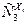
| ||||
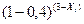
| 0.216 | 0.36 | 0.6 | |
| pi | 0.216 | 0.432 | 0.288 | 0.064 |
| F(x) | 0+0.216=0.216 | 0.216+0.432=0.648 | 0.648+0.288=0.936 |
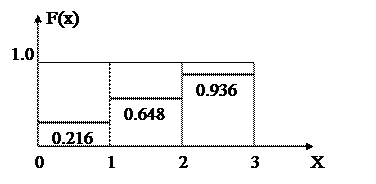
Математическое ожидание
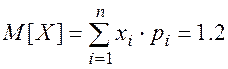
Дисперсия
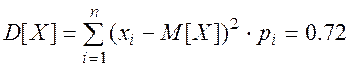 ;
;
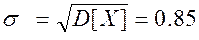
Третий центральный момент
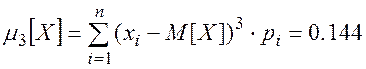
Дата добавления: 2015-05-26; просмотров: 945;
