Задача 2.25.
В течение времени t эксплуатируется N приборов. Каждый прибор имеет надежность р и выходит из строя независимо от других. Найти вероятность Р(А) того, что мастер, вызванный по окончании времени t для ремонта неисправных приборов, не справится со своей задачей за время t, если на ремонт каждого прибора мастеру требуется время t0.
Решение.
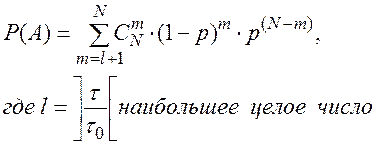
Случайные величины. Законы распределения. Числовые характеристики случайных величин.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Функцией распределения случайной величины X называется функция F(x), выражающая вероятность того, что случайная величина X примет значение меньше, чем константа x:
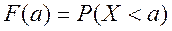 (2.20)
(2.20)
Функция F (x) есть неубывающая функция, F ( - ¥ ) = 0, F ( + ¥ ) = 1.
Плотностью распределения случайной величины называется функция
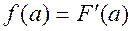 (2.21)
(2.21)
Плотность распределения любой случайной величины неотрицательна:
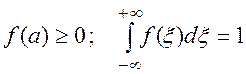 (2.22)
(2.22)
График плотности f(а) называется кривой распределения.
Элементом вероятности для случайной величины X называется величина f(а)dа, приближенно выражающая вероятность попадания случайной точки X в элементарный отрезок dа, примыкающий к этой точке.
Функция распределения случайной величины F(а) выражается через плотность распределения формулой:
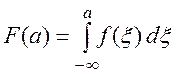 (2.23)
(2.23)
Вероятность W попадания случайной величины X на участок, протяженностью от a до b, включая a, выражается формулой:
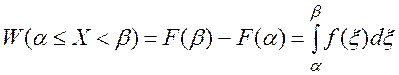 (2.24)
(2.24)
Математическим ожиданием случайной величины X называется ее среднее значение, вычисляемое по формулам:
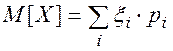 (2.25)
(2.25)
для дискретных случайных величин,
где xi –– значение случайной величины,
рi –– вероятность реализации значения xI .
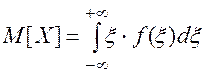 (2.26)
(2.26)
для непрерывных случайных величин
Дисперсией случайной величины называется математическое ожидание квадрата соответствующей центрированной случайной величины.
Для дискретных случайных величин:
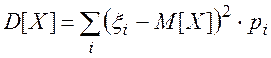 (2.27)
(2.27)
Для непрерывных случайных величин:
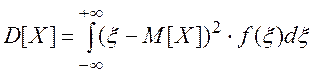 (2.28)
(2.28)
Средним квадратическим отклонением случайной величины X называется корень квадратный из дисперсии
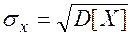 (2.29)
(2.29)
Центрированной случайной величиной 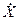 называется разность между случайной величиной Х и ее математическим ожиданием mx:
называется разность между случайной величиной Х и ее математическим ожиданием mx:
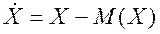 (2.30)
(2.30)
Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-й степени этой случайной величины:
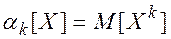 (2.31)
(2.31)
Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-й степени центрированной случайной величины:
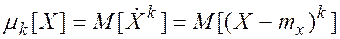 (2.32)
(2.32)
Биномиальный закон распределения числа n появления события A в n независимых опытах.
Дискретная случайная величина X называется распределенной по биномиальному закону, если она может принимать значения 0,1,2,…n, а вероятность того, что X = m < n выражается формулой:
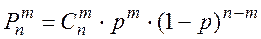 (2.33)
(2.33)
где 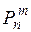 –– вероятность появления m событий при проведении n испытаний,
–– вероятность появления m событий при проведении n испытаний,
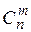 –– число сочетаний из n по m,
–– число сочетаний из n по m,
p –– вероятность появления события А в одном испытании;
q = 1-p –– вероятность непоявления события А.
Биномиальное распределение отличается следующими свойствами:
математическое ожидание числа событий (при проведении n испытаний) равно М[X] = n×p;
среднеквадратическое отклонение
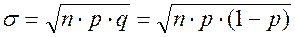 (2.34)
(2.34)
При увеличении числа испытаний биномиальное распределение приближается к нормальному со средним значением:
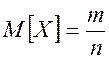 (2.35)
(2.35)
и дисперсией
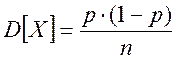 (2.36)
(2.36)
Закон Пуассона.
Дискретная случайная величина X называется распределенной по закону Пуассона, если ее возможные значения 0, 1, 2,…, n,…, а вероятность того, что X=n выражается зависимостью:
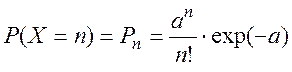 (2.37)
(2.37)
где a > 0 –– параметр закона Пуассона.
Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, вычисляются по формулам:
 (2.38)
(2.38)
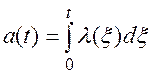 (2.39)
(2.39)
где l(x) –– функция интенсивности появления случайного события.
Вероятность числа n реализаций за время t случайных событий, распределенных по закону Пуассона, при l(t) = const = l вычисляется по формуле:
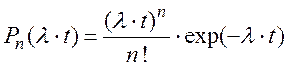 (2.40)
(2.40)
где l –– интенсивность появления случайного события, равная среднему числу реализации событий в единицу времени;
l×t = а –– среднее число событий, реализовавшихся за время t.
Характерным признаком распределения Пуассона является равенство математического ожидания и дисперсии
(М[X] = l×t, D[X] = l×t).
Функция вида:
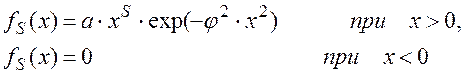 (2.41)
(2.41)
где a>0, j>0 –– некоторые постоянные,
S –– натуральное число
обладает свойствами плотности распределения. Некоторые из законов распределения случайных величин типа fS(x) имеют определенные названия, например:
f1(x) –– называется законом Релея,
f2(x) –– называется законом Максвелла.
Для закона Релея:
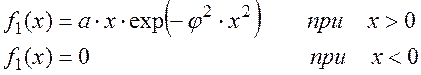 (2.42)
(2.42)
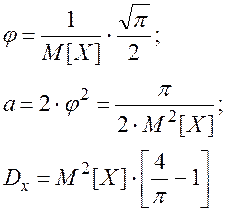 (2.43)
(2.43)
Для закона Максвелла:
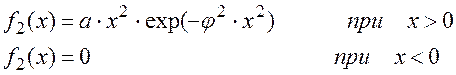 (2.44)
(2.44)
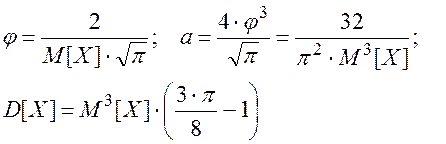 (2.45)
(2.45)
Все законы вида:
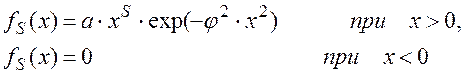 (2.46)
(2.46)
являются однопараметрическими, т.е. зависят только от одного параметра, в качестве которого можно задать, например, математическое ожидание или дисперсию.
Равномерный закон распределения непрерывной случайной величины.
Непрерывная случайная величина X называется равномерно распределенной в интервале ( a, b ), если ее плотность распределения на этом интервале постоянна:
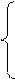
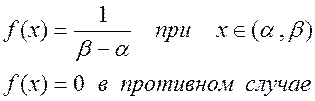 (2.47)
(2.47)
Математическое ожидание и дисперсия случайной величины при ее равномерном распределении соответственно равны:
 (2.48)
(2.48)
Вывод формулы (2.48).
По определению:
дисперсия 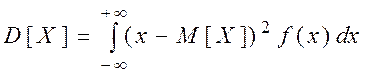
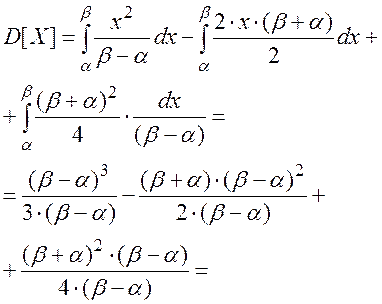 |
Поскольку случайная величина распределена равномерно на интервале (a, b), то:
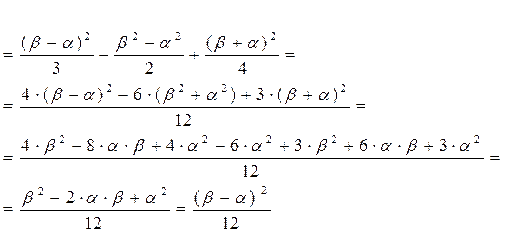
Нормальный закон распределения случайных величин.
Непрерывная случайная величина X называется распределенной по нормальному закону, если плотность ее распределения подчинена зависимости:
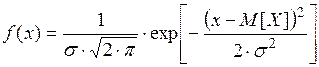 (2.49)
(2.49)
где: m –– математическое ожидание случайной величины;
D = s2 –– ее дисперсия.
Вероятность попадания случайной величины X , распределенной по нормальному закону, в интервале (a, b) выражается формулой:
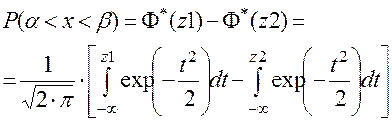 (2.50)
(2.50)
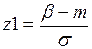 (2.51)
(2.51)
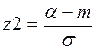 (2.52)
(2.52)
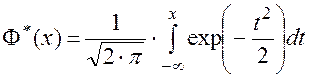 (2.53)
(2.53)
Функция Ф*(x) –– табулированная функция Лапласа.
На практике удобнее пользоваться аппроксимацией Ф.А. Евстифеева.
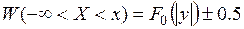 (2.54)
(2.54)
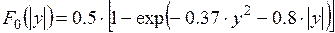 (2.55)
(2.55)
где 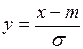 –– нормированное отклонение случайной величины Х.
–– нормированное отклонение случайной величины Х.
В (2.55) принимается знак (-), если величина y отрицательна и (+) в противном случае.
Распределение Вейбулла.
Плотность распределения:
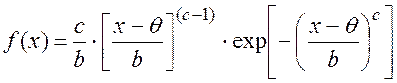 (2.56)
(2.56)
где 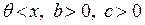
Функция распределения (функция отказов или ненадежности):
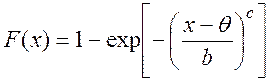 (2.57)
(2.57)
Функция надежности:
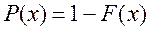
Интенсивность отказов:
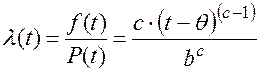 (2.58)
(2.58)
Для начального этапа эксплуатации технических систем распределение Вейбулла используется для расчета вероятности безотказной работы системы в течение времени t. Для этих целей можно принять значения:
q = 0, b ³ 1, c @ 0.5, tÎ[0, t1]
где t1 –– окончание этапа приработки технической системы.
Ниже приведен пример изменения интенсивности отказов (2.58), подчиненных распределению Вейбулла с определенными выше значениями констант.
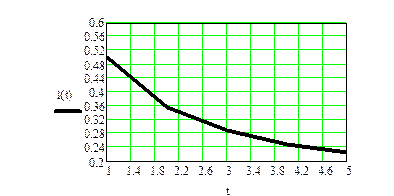
Рис. 2.2.1. Изменение интенсивности отказов на начальном этапе эксплуатации системы.
Дата добавления: 2015-05-26; просмотров: 1863;
