Тепловая теорема Нернста.

Прямой и простой расчет изменения энергии Гиббса, а, следовательно, и констант равновесия химических реакций не вызывает затруднений, если известны теплота химической реакции и абсолютные значения энтропии всех участников реакции. Постулат Планка дает такую возможность, т.е. возможность вычисления абсолютных значений энтропии индивидуальных веществ при любой температуре.

Тепловая теорема Нернста исторически предшествовала названному постулату и относится к тому периоду в развитии термодинамики, когда решение задачи об определении изменения энергии Гиббса реакции было связано с определенными трудностями.

Для расчета DG реакции - главной цели учения о химическом равновесии – требовались опытные определения:

- теплового эффекта реакции при какой-нибудь одной температуре

- теплоемкостей в широком интервале температур

- констант равновесия при разных температурах для того, чтобы определить значение константы интегрирования I в уравнении (III, 36).

Получаемое в конечном результате уравнение 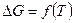могло быть применимо в тех пределах температур, в которых определены теплоемкости и константы равновесия. Описанный нами путь являлся безукоризненным с опытной точки зрения; точность конечных расчетов полностью зависела от точности опытных данных. Очевидно, что весь этот путь являлся сугубо эмпирическим и притом очень трудоемким.

Нернст отчетливо поставил цель облегчить его теоретическими моментами. Рассуждения сводилась к следующему. Для вычисления DG химической реакции надо:

- опытным путем определить тепловой эффект реакции при какой-нибудь одной температуре

- опытным путем определить теплоемкости в широком интервале температур

- создать теорию теплоемкости для того, чтобы избежать эмпирических формул зависимости теплоемкостей от температуры

- вывести уравнение для вычисления DG химической реакции непосредственно из уравнения Гиббса-Гельмгольца, совершенно не прибегая к опытным определениям констант равновесия.

Создать теорию теплоемкости, которая бы количественно отображала действительные соотношения, не удалось.

Тем не менее, мысль Нернста вывести уравнения DG химической реакции непосредственно из уравнения Гиббса-Гельмгольца

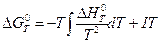(V,14)

представляла особый интерес.

Очевидно, что для вычисления DG по этой формуле надо знать кроме зависимости 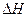от Т, по меньшей мере значение DG при какой-либо одной температуре, чтобы определить константу интегрирования I. Наличие этой неопределенности в качестве решения уравнения (V,14) дает семейство кривых (смотри рис.10 , на котором это семейство кривых обозначено пунктирными линиями).

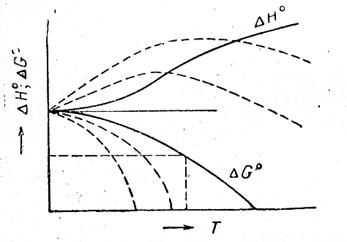
Рис.10. Зависимость теплового эффекта и изменения энергии Гиббса химической реакции от температуры.

Причем, только одна из кривых является истинной (на рис. она обозначена сплошной линией), т.к. энергия Гиббса – однозначная функция параметров состояния системы.

Руководствуясь рядом опытных указаний, Нернст высказал следующую гипотезу, получившую название тепловой теоремы Нернста: вблизи абсолютного нуля для конденсированных систем не только

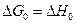, но и

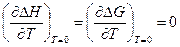(V,15)

Графически это означает, что кривые DG и 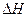при абсолютном нуле соприкасаются, т.е. имеют общую касательную, причем эта касательная параллельна оси абсцисс (температур). Следовательно, из всего семейства кривых 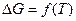реальной является та кривая, касательная которой при Т = 0 горизонтальна.

Если мы, как и раньше, представим 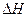в виде

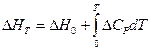
где 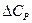- разность теплоемкостей продуктов реакции и исходных веществ, находящихся в конденсированном состоянии, то после подстановки в уравнение (V,14) получим:

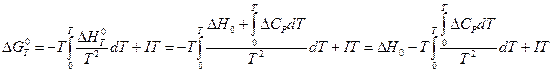(V,16)

Берем теперь производную DG по Т, причем средний член справа в (V,16) дифференцируем как произведение:

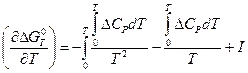(V,17)

(при дифференцировании 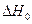обращается в нуль, т.к. является константой и не зависит от температуры).

При переходе к пределу 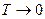учитывается тот факт, что 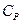, а значит и 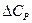пропорциональны 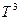по закону Т-кубов Дебая (смотри (I, 20)). Тогда при приближении к 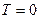оба первых члена в правой стороне уравнения (V,17) обращаются в нуль. С учетом (V,15) получаем:

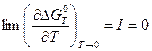
Следовательно, при температурах, близких к абсолютному нулю, константа интегрирования I в уравнении Гиббса-Гельмгольца также обращается в нуль.

Таким образом, для реакций в конденсированных системах в области абсолютного нуля уравнение (V,16) переходит в уравнение:

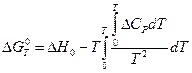
Опираясь на тепловую теорему Нернста, был сделан ряд важных и интересных заключений относительно энтропии твердых тел.

Т.к. в соответствии с (III, 26а)

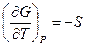, то при Т = 0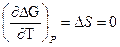

иными словами, процессы, протекающие в системе при абсолютно нуле, не изменяют ее энтропии.

Планк расширил этот вывод, допустив, что энтропия всякого однородного кристаллического вещества равна нулю, т.е.

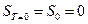
Теорему Нернста в сочетании с гипотезой Планка, касающейся значения энтропии в нулевой точке, принято называть третьим законом (началом) термодинамики (смотри § 4 второй главы).