Методы расчета коэффициента летучести.

Чтобы вычислить летучесть, необходимо знать явную зависимость ее от давления при постоянной температуре.

Энергия Гиббса как функция давления и температуры определяется по уравнению ()

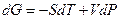
Тогда при T = const оно сводится к виду .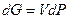

Интегрирование этого уравнения дает следующий результат:

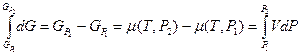
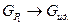Если , то свойства газа приближаются к свойствам идеального газа, т.е. . Опуская индекс «2», в этом случае можем записать:

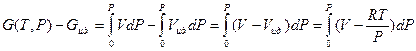, (V,22)

с учетом выражения 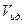для одного моля идеального газа из уравнения Менделеева – Клапейрона.

Если принять во внимание, что для одного моля вещества в газообразном состоянии

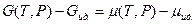(V,23)

то подставив из (V,18) и (III,46) значения химического потенциала для реального и идеального газов, получим:

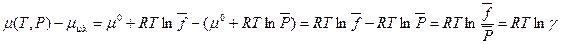( V,24)

Из сравнения уравнений (V,22), (V,23) и (V,24)следует, что

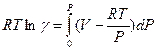
Или после простых преобразований:

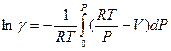(V,25)

Разность 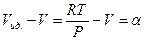- это так называемая объемная поправка неидеального газа, учитывающая, что объем реального газа отличается от объема идеального газа.

С учетом введенного обозначения уравнение (V,25) можно переписать следующим образом:

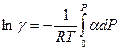(V,26)

Полученное уравнение позволяет вычислять коэффициенты летучести по экспериментальным данным. Величину интеграла находят графически по площади под кривой 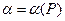(смотри рис. )

Другой графический метод расчета основан на использовании коэффициента сжимаемости. Коэффициентом сжимаемости z называется отношение 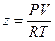. Очевидно, что для идеального газа его значение равно единице, но отличается от единицы для реальных газов.

Если принять во внимание, что

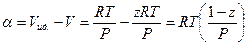
уравнение (V,26) можно преобразовать к следующему виду:

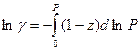
Полученный интеграл определяют графически по площади под кривой в координатах

(z – 1) – lnP.

Третий метод используют для определения коэффициента летучести по изотермам идеального и реального газов в координатах P – V от достаточно низкого давления, при котором эти изотермы практически сливаются, до давления, при котором требуется определить летучесть. Интеграл в правой части уравнения (V,25) определяют графически (смотри рис. ).

Еще один метод определения коэффициентов летучести основан на принципе соответственных состояний (метод Ньютона). Согласно этому принципу при одинаковых приведенном давлении 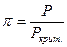и приведенной температуре 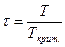значения коэффициента летучести для различных веществ должны быть одинаковыми. Из понятия соответственного состояния вытекает, что коэффициент сжимаемости z, который учитывает степень отклонения неидеальных систем от идеальной, в критическом состоянии для всех веществ должен быть одинаков: .

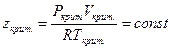В действительности же, его величина зависит от природы вещества. На этом основании составлены таблицы, где при определении значений коэффициентов летучести учитываются не только приведенные температура и давление, но и различные значения 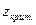. Таким образом, при близости вещества к насыщенному состоянию .

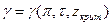Зависимость коэффициента летучести от приведенного давления при различных приведенных температурах и значениях 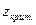может быть представлена на графиках, используемых для тех же определений (смотри рис. ).

§ 10. Зависимость энтальпии веществ и тепловых эффектов химических реакций от давления.

При рассмотрении зависимости энтальпии от давления воспользуемся ее определением .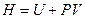

Продифференцируем это выражение по давлению при условии постоянства температуры:

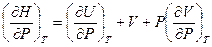(V,27)

Теперь запишем известное нам выражение для dU:

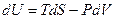
Разделим его на dP при условии постоянства температуры

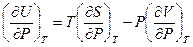(V,28)

Теперь, если принять во внимание соотношение Максвелла (III.32), согласно которому 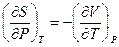и подставить его в (V,28), получим:

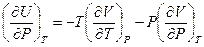(V,29)

Это выражение подставим в (V,27) и после сокращений запишем

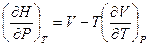
Если обе части последнего уравнения умножить на dP и проинтегрировать от Р = 1 атм. до Р при T = const, то это позволит определить абсолютную энтальпию вещества

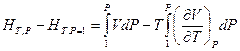или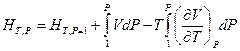

Аналогичное выражение можно записать для теплового эффекта химической реакции:

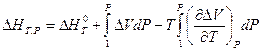
где 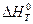- тепловой эффект химической реакции при стандартных условиях, а 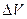- изменение объема системы в результате реакции.

Теплоту реакции при любом давлении можно вычислить из полученного уравнения, если экспериментальные данные позволяют вычислить интегралы в его правой части.

Однако на практике поступают иначе, используя значения функции 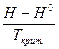для веществ, участвующих в реакции. Она зависит от приведенных температуры и давления. Ее значение, которое дается в виде графиков или таблиц, позволяет учесть изменение энтальпии с изменением давления, а затем рассчитать тепловой эффект химической реакции при заданных условиях.

[1] Все сказанное выше относительно испарения действительно и для процесса возгонки (сублимации).