Тежное сопротивление

В теории напряженного состояния решаются две основные задачи:

- Первая задача ТНС:

По известному напряженному состоянию в точке определить нормальное σ_α и касательное t_α напряжения на любой наклонной площадке.

- Вторая задача ТНС:

По известному напряженному состоянию в точке найти положения главных площадок и значения главных напряжений

Напряжения на наклонных площадках

- одноосное напряженное состояние

(6.2)

- двуосное напряженное состояние

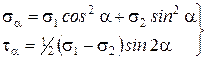(6.3)

- обобщенное плоское напряженное состояние

(6.4)

- чистый сдвиг

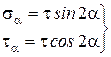(6.4)

- общий случай объемного напряженного состояния

(6.5)

где l ,m, n - направляющие косинусы нормали к наклонной площадке

Положение главных площадок при обобщенном плоском напряженном состоянии определяется по формуле:

(6.6)

Главные напряжения в этом случае находятся по формуле:

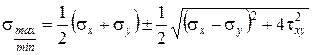(6.7)

Максимальные касательные напряжения равны:

- при одноосном н.с. : _max = ½  (6.8)

- при плоском н.с. : _max = ½ (_max – _min) (6.9)

Прочность в опасной точке проверяется по одной из теорий прочности в зависимости от вида Н.С. и материала стержня

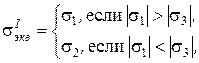- (6.10)

- , где  - коэффициент Пуассона (6.11)

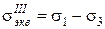- , (6.12)

- , (6.13)

Связь между напряжениями и деформациями выражается в виде закона Гука:

- одноосное Н.С. : , ¢ = –   (6.15)

- двуосное Н.С. : (6.16)

- чистый сдвиг : , (6.17)

- обобщенное плоское Н.С. : (6.18)

- трехосное Н.С. : 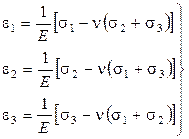(6.19)

- общий случай объемного н.с. :