Тема 5 Изгиб.

§5.1Основные понятия. Поперечная сила Q_y. Изгибающий момент М_х.

Изгибом называется вид сопротивления, при котором изменяется кривизна оси стержня. Прямой стержень, испытывающий прямой изгиб называется балкой.

Балка соединяется с неподвижной поверхностью с помощью опорных устройств. Различают следующие виды опорных устройств.

· Шарнирно-неподвижная (В)
и шарнирно-подвижная (С) опоры

· Жесткая заделка

Рисунок 5.1

Реакции опорных устройств находятся из условий равновесия.

Внутренние усилия в поперечных сечениях балок приводятся к двум составляющим – поперечной силе Q_y и изгибающему моменту М_х.

· Поперечная сила Q_y в данном сечении балки равна алгебраической сумме внешних сил, действующих по одну сторону от проведенного сечения перпендикулярно недеформированной оси балки .

Правило знаков для Q_y

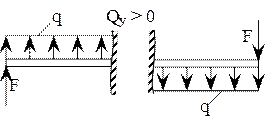
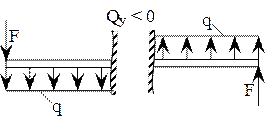
Рисунок 5.2

· Изгибающий момент M_х в данном сечении балки равен алгебраической сумме моментов относительно центра тяжести проведенного сечения внешних сил, действующих по одну сторону от проведенного сечения.

Правило знаков для M_х

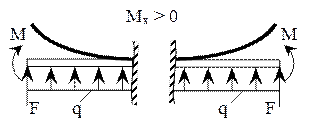
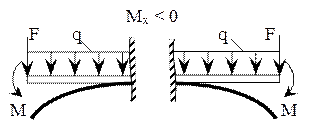
Рисунок 5.3

Между поперечной силой Q_y, изгибающим моментом М_х и интенсивностью равномерно нагрузки q существуют следующие дифференциальные зависимости:

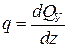, (5.1)

Графики, показывающие изменение Q_y и М_х по длине балки, называют эпюрами Q_y и М_х. как и ранее, эпюры строятся на базовых линиях, параллельных оси стрежня, ординаты эпюр перпендикулярны базовой линии. положительные ординаты откладываются по одну сторону от базовой линии, отрицательные – по другую.

§5.2 Напряжения при изгибе: нормальные, касательные, главные. Расчеты на прочность при изгибе

Распределенные нормальные s и касательные напряжения t при изгибе определяются формулами:

· Навье

(5.2)

· Журавского

(5.3)

Рисунок 5.12

где Q_у, М_х – поперечная сила и изгибающий момент в данном сечении;

у – расстояние от исследуемой точки до нейтральной линии;

J_x – момент инерции сечения относительно нейтральной линии;

– статический момент относительно до нейтральной линии площади, отсекаемой на уровне исследуемой точки со стороны противоположной нейтральной линии;

b(у) – ширина поперечного сечения на уровне исследуемой точки;

Эпюры s и t, построенные по формулам (5.2) и (5.3), показывают, что напряжения распределяются неравномерно, вследствие этого в отдельных элементах материала балки наблюдаются различные напряженное состояние.

Точка К₁ – наивысшая точки сечения:

(5.4)

Так как напряженное состояние в точке К₁ – одноосное, то условие прочности имеет вид:

(5.5)

Точка К₂ – точка на нейтральной линии сечения:

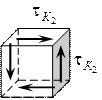
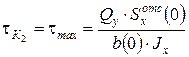(5.6)

Так как напряженное состояние в точке К₂ – чистый сдвиг, то условие прочности имеет вид:

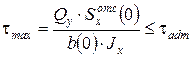(5.7)

Точка К₃ – произвольная точка поперечного сечения:

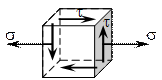
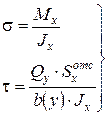(5.8)

Ищем главные напряжения:

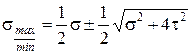(5.9)

Условие прочности по пяти теориям прочности:

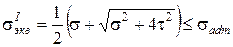(5.10)

(5.11)

(5.12)

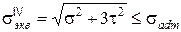(5.13)

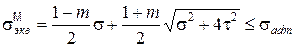, где (5.14)

Условие (5.5) называется условием прочности по нормальным напряжениям,
(5.7) – условие прочности по касательным напряжениям;
(5.9) - (5.14) – условие прочности по главным напряжениям.

Проектировочный расчет осуществляют с использованием (5.5) с последующей проверкой его по (5.7) и одной из (5.10)-(5.14).

Проверка прочности по (5.5), (5.7) и одной из (5.10)-(5.14) называется полной проверкой прочности.