Тема 3 Геометрические характеристики плоских сечений

Основные понятия

Сопротивление стержня различным видам нагружения определяется не только размерами поперечного сечения, но и в значительной степени расположением сечения относительно линии действия внешних сил. Расположение плоского сечения относительно координатных осей учитывается геометрическими характеристиками: статический момент площади, осевые, полярный и центробежный моменты инерции.

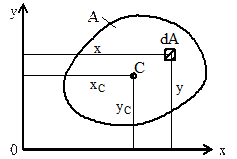Статические моменты площади Аэто

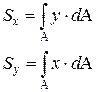(2.1)

где dA –элементарная площадь,

x, y – координаты элементарной площади.

Размерность статического момента – единица длины в третьей степени.

Если x_с, y_с – координаты центра тяжести, то статические моменты площади А

S_x = A × y_c S_y = A × x_c (2.2)

В случае сложного сечения статический момент равен алгебраической сумме статических моментов простых сечений, на которые делится заданное сложное сечение.

Осевые моменты инерции (моменты инерции относительно координатных осей) плоского сечения это:

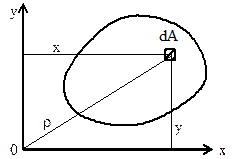
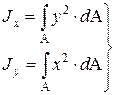
Полярный момент инерции плоского сечения это:

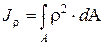
Осевые и полярный моменты инерции связаны следующей зависимостью: J_r = J_x+ J_y

Центробежный момент инерции это: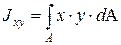

Размерность всех моментов инерции – единица длины в четвертой степени.

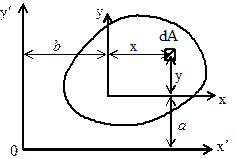Если координаты элементарной площади dAотносительно параллельных осей связаны зависимостью:

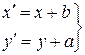
то зависимости между моментами инерции плоского сечения относительно параллельных осей следующие:

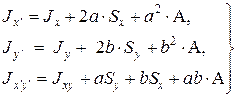
Если начальные оси x, y – центральные, то (2.7) примет вид:

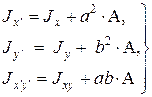
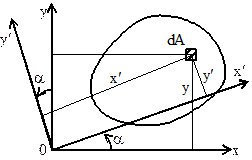Если оси x¢, y¢ получены поворотом начальных координатных осей x, y вокруг начала координат О на угол a, то моменты инерции плоского сечения относительно новых осей x¢, y¢ равны:

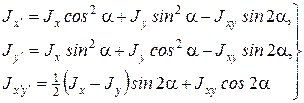
Оси относительно которых а)осевые моменты инерции достигают экстремальных значений, б)центробежный момент инерции равен нулю называются главными осями инерции.

Положение главных моментов инерции определяются формулами:

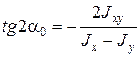
Значения главных моментов инерции определяются формулами:

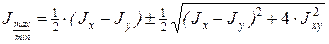
Тема 4 Кручение. Основные понятия. Напряжения и перемещения
при кручении. Расчеты на прочность и жесткость

Кручением называется вид нагружения, при котором под действием внешних сил в поперечных сечениях стержня (вала) возникает единственный внутренний силовой фактор – крутящий момент Т. Т.к кручение вызывается внешними парами сил (моментами), действующими в плоскостях поперечных сечений, то крутящий момент Т в произвольном сечении стержня (вала) равен алгебраической сумме внешних моментов, действующих по одну сторону от рассматриваемого сечения. Крутящий момент Т > 0, если глядя со стороны сечения, мы видим вращение отсеченной части вокруг оси стержня против часовой стрелки. График, показывающий изменение крутящего момента Т по длине вала, называется эпюрой. Правила построения эпюры Т:

- эпюра строится на базовой линии, параллельной оси вала,

- ординаты эпюры откладываются по нормали к базовой линии, положительные по одну сторону, отрицательные по другую.

Иногда в условии задачи вместо передаваемого момента задаются передаваемая мощность Р и скорость вращения. Передаваемый момент вычисляется так:

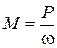- , если Р – в Вт и w - в рад/с;

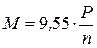- , если Р – в Вт и n - в об/мин;

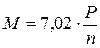- , если Р – в л.с. и n - в об/мин.

Кручение стержня круглого поперечного сечения

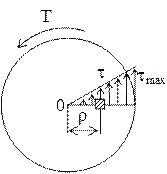
В поперечных сечениях скручиваемого стержня (вала) действуют касательные напряжения t, изменяющиеся по линейному закону

,

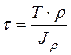где Т – крутящий момент в сечении;

r – расстояние от центра сечения до данной точки;

J_r - полярный момент инерции.

Рисунок 3.1

Для круга 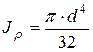, где d – диаметр сечения:

Для кольца ,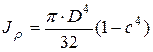

где D – наружный диаметр кольца;

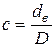– отношение внутреннего диаметра к наружному.

Максимальные касательные напряжения будут на контуре сечения

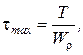(3.2)

где W_r – полярный момент сопротивления сечения.

Для круга ,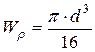

Для кольца .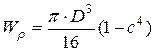

Условие прочности при кручении

Для того , чтобы прочность скручиваемого вала была обеспечена, необходимо и достаточно, чтобы максимальные касательные напряжения не превышали допустимых значений

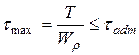, (3.3)

При кручении t_мах = (0,5-0,6)s_adm.

Для проведения расчетов на жесткость определяют угол закручивания j, который подчиняется дифференциальному уравнению

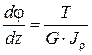, (3.4)

гдеGJ_r – жесткость поперечного сечения при кручении.

– если 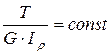, то 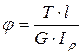, (3.5)

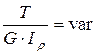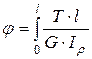– если , то (3.6)

Условие жесткости при кручении

Для того , чтобы жесткость скручиваемого вала была обеспечена, необходимо и достаточно, чтобы максимальный угол закручивания не превышал допустимого значения

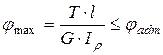, (3.7)

Допускаемый угол закручивания зависит от назначения рассчитываемого вала. Единых норм жесткости, общих для различных отраслей машиностроения, не существует. Наиболее распространенные значения допускаемых углов закручивания (относительных ).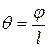

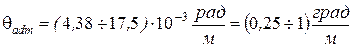
Формулы для вычисления диаметра вала из условий прочности и жесткости можно свести в следующую таблицу:

	Сплошной вал	Полый вал
Из условия прочности		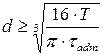D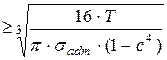
Из условия жесткости		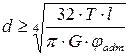D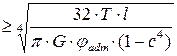

Стержень некруглого поперечного сечения

В случае некруглых сечений расчеты проводится по специальным формулам из теории упругости.

Ниже приводятся эти формулы для прямоугольного сечения.

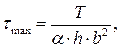(3.9).

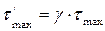(3.10).

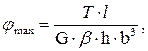(3.11).

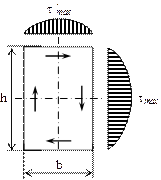
Рисунок 3.2

В (3.9)-(3.11) b, h - стороны прямоугольного сечения; a, b, g -безразмерные коэффициенты, зависящие от отношения .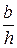

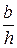
		1,2	1,4	1,6	1,8	2,0	2,5	3,0	4,0	6,0	8,0	10,0 и более
a	0,208	0,219	0,228	0,234	0,240	0,246	0,258	0,267	0,282	0,299	0,307	0,333
b	0,140	0,166	0,187	0,204	0,217	0,229	0,249	0,263	0,281	0,299	0,307	0,333
g	1,000	0,932	0,865	0,845	0,821	0,796	0,774	0,753	0,745	0,743	0,743	0,743

Расчет на кручение стержня прямоугольного сечения встречается довольно часто при сложном сопротивлении