Тема 2 Центральное растяжение и сжатие

Основные понятия и определения

При центральном растяжении и сжатии в поперечных сечениях стержня возникает единственный внутренний силовой фактор – продольная сила N.
В произвольном сечении стержня продольная сила N численно равна алгебраической сумме проекций на продольную ось стержня всех внешних сил, действующих по одну сторону от проведенного сечения.

При растяжении продольную силу N будем считать положительной, при сжатии – отрицательной.

Для расчета на прочность и определения перемещений поперечных сечений стержня надо знать закон изменения продольных сил по его длине. Изменение продольной силы по длине стержня можно представить в виде эпюры.

Нормальные напряжения s в поперечном сечении стержня

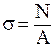(1.1)

где N – продольная сила, н

А – площадь поперечного сечения, мм²

Знак s зависит от знака N, т.е. при растяжении s > 0, при сжатии s < 0.

Абсолютным удлинением называют разность между длинами стержня после и до деформации:

Dl = l' – l (1.2)

где Dl – абсолютное удлинение, мм;

l' и l – длины стержня после и до деформации, мм.

Удлинение, приходящееся на единицу длины стержня, называется относительной продольной деформацией:

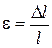(1.3)

Зависимость между продольной деформацией e и нормальным напряжением sвыражается законом Гука:

s =e × E (1.4)

где E – модуль упругости І рода или модуль Юнга, н/мм².

Закон Гука для абсолютного удлинения выражается формулой

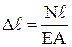(1.5)

Величина EA называется жесткостью поперечного сечения при растяжении и сжатии.

Поперечная деформация e' стержня определяется зависимостью

e' = –n × e (1.6)

где n – коэффициент Пуассона.

Условие прочности при растяжении и сжатии имеет вид

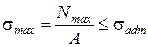(1.7)

где s_adm – допускаемое напряжение, н/мм².

Условие жесткости при растяжении и сжатии имеет вид:

Dl £ Dl_adm(1.8)

где Dl_adm – допускаемое удлинение, мм.

На основании (1.7) и (1.8) можно решать задачи трех типов:

1) Проверочный расчет