Метод сечений. Внутренние усилия

Решение основных задач сопротивления материалов невозможно без определения внутренних сил. Внутренние силы находят методом сечений. Последовательность следующая:

а) Р – разрезаем стержень некоторой плоскостью

б) О – отбрасываем одну часть (мысленно)

в) У – уравновешиваем оставшиеся внешние силы внутренними силами, возникающими в проведенном сечении между частицами материала;

г) П – приводим внутренние силы в данном сечении к эквивалентным главному вектору 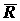и главному моменту 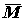(центр приведен – центр тяжести).

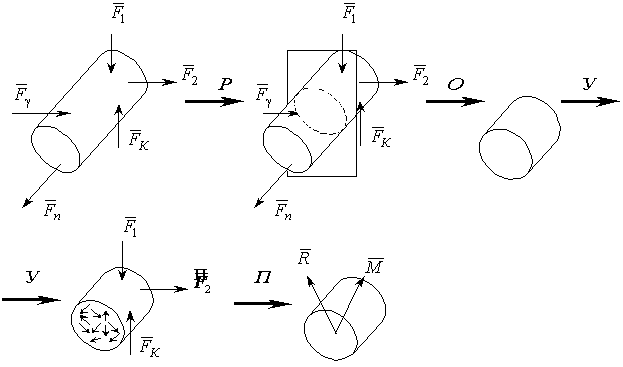
Рис. 1.1.

Разложим главный вектор 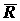и главный момент 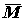на составляющие вдоль координатных осей. Начало координат выберем в центре тяжести сечения, ось z направим по нормали к сечению, а оси х, у – в плоскости сечения.

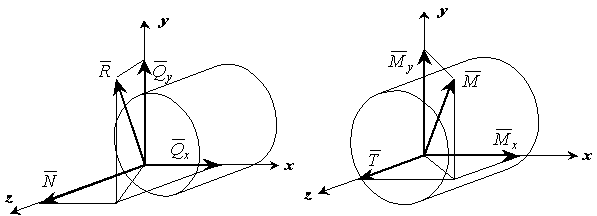
Рис. 1.2.

Обозначим составляющие главного вектора и главного момента – N, Q_x, Q_y, T, M_x, M_y. Для этих составляющих приняты следующие названия: N – продольная сила; Q_x, Q_y - поперечные силы, Т – крутящий момент; M_x, M_y – изгибающие моменты. Эти 6 величин называются внутренними силовыми факторами (В.С.Ф.).

Рассмотрим равновесие отсеченной части под действием внешних сил и В.С.Ф.

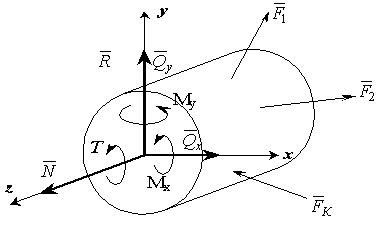
Рис. 1.3

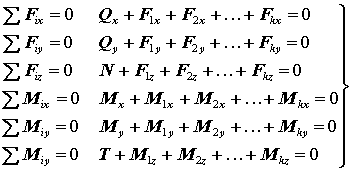(1.1)

Из уравнений (1.1) найдем все шесть В.С.Ф. Следуем отметить, что учитываются внешние силы, действующие только с одной стороны от проведенного сечения. Каждый из шести В.С.Ф. связан с определенным видом сопротивления (деформации) сжатия.

Таблица 1.1