Косой изгиб
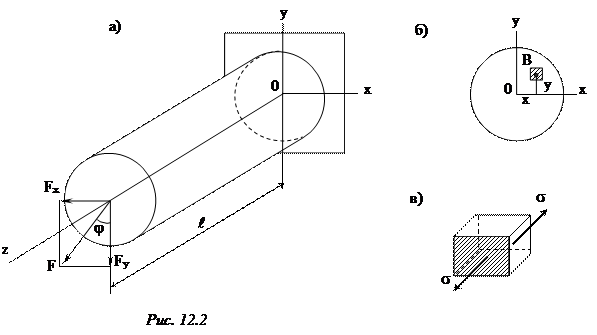 |
Внешние силы, моменты, распределенные нагрузки, действующие в разных плоскостях, проходящих через ось стержня, вызывают пространственный или косой изгиб. Искривленная ось стержня является пространственной кривой. При решении задачи об определений напряжений и перемещений удобно пользоваться разложением пространственного изгиба на два плоских – в плоскостях хОz и yOz.
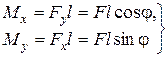 (7.1) В произвольной точке В(х, у) нормальные напряжения будут:
(7.1) В произвольной точке В(х, у) нормальные напряжения будут:
 (7.2)
(7.2)
С учетом (12.2):
 (7.3) (12.4)
(7.3) (12.4)
В (7.2) и (7.3) Jx, Jy – главные центральные моменты инерции поперечного сечения. Напряженное состояние в исследуемой точке – одноосное (рис. В). Следовательно, опасной является точка, в которой s достигает наибольшего значения.
Согласно (7.2) и (7.3) s распределяется по линейному закону. Для определения опасной точки используем нейтральную линию. Т.к. на нейтральной линии s=0, то уравнение нейтральной линии имеет вид:
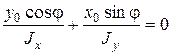 (7.4)
(7.4)
где х0, у0 – координаты точек нейтральной линии. Если a - угол между нейтральной линией и осью х, то:
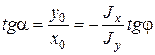 (7.5)
(7.5)
 (7.4) – уравнение нейтральной линии, выраженное через угловой коэффициент. Согласно (7.5):
(7.4) – уравнение нейтральной линии, выраженное через угловой коэффициент. Согласно (7.5):
1) нейтральная линия, как и силовая, проходит через центр тяжести поперечного сечения;
2) нейтральная и силовая линия, проходят через разные четверти;
3) нейтральная линия не перпендикулярна силовой (в отличие от плоского изгиба).
Исключение: квадрат, круг, т.е. сечения у которых Jx = Jy.
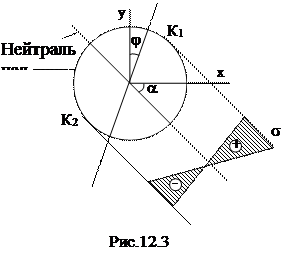
Покажем положение нейтральной линии (рис. 12.3) и используем ее для определения опасной точки. Очевидно, это точки контура сечения, в которых касательные к контуру параллельны нейтральной линии. Обозначим, т. К1 – точка на контуре сечения в зоне растянутых волокон, т. К2 – точка на контуре в зоне сжатых волокон. Итак:
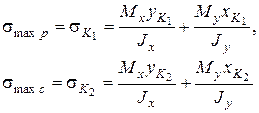 (7.6)
(7.6)
Здесь используется формула (7.2) как имеющая более общий вид ((7.3) справедлива только при действии одной силы F).
Если контур сечения имеет выступающие точки, то опасными будут являться выступающие точки контура.
Зная (7.6), в зависимости от вида материала можно составить условие прочности:
а) пластичный материал

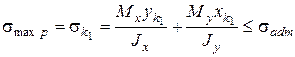 (7.7)
(7.7)
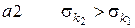
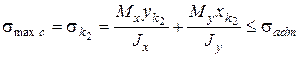 (7.8)
(7.8)
б) хрупкий материал
 (7.9)
(7.9)
Для прямоугольного, двутаврового сечений
 (7.10)
(7.10)
Поэтому условие прочности для таких сечений можно представить в виде:
 (7.11)
(7.11)
При косом изгибе ограничиваются определением прогибов. Полный прогиб находиться как геометрическая сумма прогибов fx, fy в главных плоскостях:
 (7.12)
(7.12)
Прогибы fx, fy находятся интегрированием дифференциальных уравнений:
 (7.13)
(7.13)
Уравнения (7.13) можно решать либо методом начальных параметров, либо по общей формуле Мора с применением правила Верещагина.
§ 7.3 Изгиб с кручением
В различных деталях машин часто встречается одновременное действие изгиба с кручением. Например, коленчатый вал, оси вагонов поездов и трамваев. Практическое значение имеют результаты при изгибе с кручением в стержнях круглого и прямоугольного поперечных сечений.
Ø 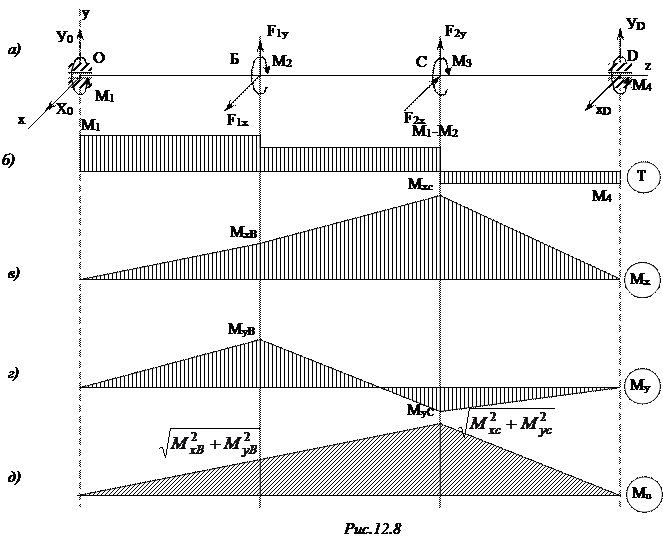
Круглое сечение
Силы, действующие на вал (давление на зубья шестерен, натяжения ремней, собственный вес вала и шкивов и т.п.) вызывают в поперечных сечениях вала следующие силовые факторы: поперечные силы Qy, Qx, изгибающие моменты Мх, Му и крутящий момент Т. Для расчета вала на прочность необходимо определить опасные сечения, для чего строятся эпюры ВСФ (рис.12.8 а-д).
При изгибе вала круглого сечения в каждом из его сечений действует изгибающий момент 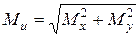 , (рис. 12.8 д).
, (рис. 12.8 д).
Изгибающий момент в разных сечениях имеет различные направления, поэтому даже при отсутствии распределенной нагрузки эпюра Ми может быть криволинейной.
По построенным эпюрам Ми и Т находим опасные сечения. Очевидно, это одно из сечений В или С. Для определения опасных точек строим эпюры напряжений и, установив опасные точки, исследуем напряженное состояние в опасных точках (рис. 12.9 а,б).
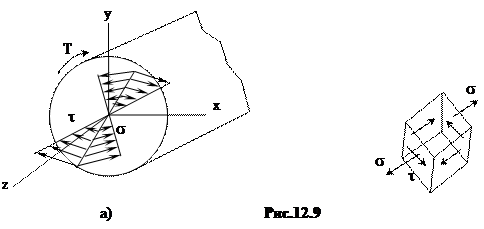 |
Эпюра s и t (рис. 12.9 а) показывают, что опасными являются точки на контуре сечения, где напряженное состояние – обобщенное плоское (рис. 12.9 б) напряжения в опасных точках:
 (7.14)
(7.14)
Для круглого сечения (и сплошного, и полого):
Wr=2Wx (7.15)
Ищем главные напряжения в опасной точке:
 (7.16)
(7.16)
Т.к. сечение круглое, то можно пренебречь касательными напряжениями от поперечных сил. Следовательно, t в (12.26) это напряжения от крутящих моментов, а s - это изгибающих моментов. Составим условие прочности по І-V теориям прочности:
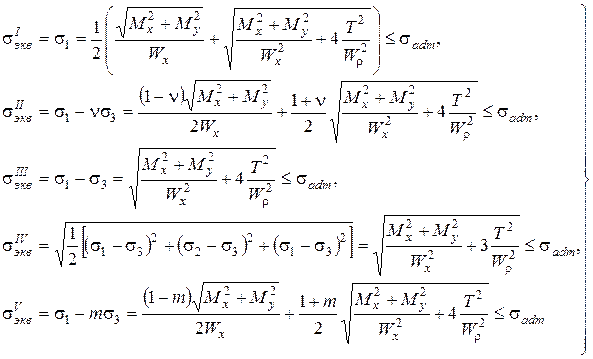
Анализ формул (7.17) показывает, что учитывая (7.15)), можно все формулы (7.17) привести к единой форме:
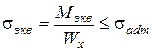 (7.18)
(7.18)
где Мэкв вычисляется в зависимости от используемой теории прочности:
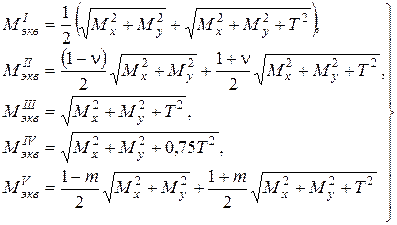 (7.19)
(7.19)
где n - коэффициент Пуассона,  . Формула (7.18) позволяет проводить все виды расчетов на прочность.
. Формула (7.18) позволяет проводить все виды расчетов на прочность.
Дата добавления: 2015-05-21; просмотров: 1891;
