Эмпирическая формула расчета на устойчивость.

Вычислим s_кр, используя (11.3):

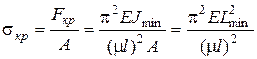, (8.4)

где 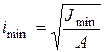- главный радиус инерции. Введем обозначение 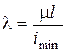и отметим, что введенная величина безразмерна, и является характеристикой стержня, зависящей от способа его закрепления и размеров (длины, формы и размеров поперечного сечения)

Введенная характеристика

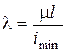(8.5)

называется гибкостью стержня. Формула Эйлера для критического напряжения с учетом обозначения (8.5) имеет вид

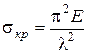(8.6)

(8.6) выполняется лишь при напряжениях, не превышающих предела пропорциональности, т.е.

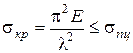(8.7)

Следовательно, формула Эйлера применима лишь для стержней, гибкость которых согласно (8.7)

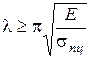. (8.8)

где 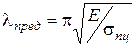называется предельной гибкостью. Отметим, что предельная гибкость стержня характеризует лишь свойства материала, из которого изготовлен стержень. Например: для сталей Ст. 2, Ст.3, Ст. 5 - l_пред = 100, сталь 40 - l_пред = 90, для дерева - l_пред =110, для чугуна - l_пред =80.

Итак, критическое напряжение можно находить по формуле Эйлера (11.6) лишь при условии, что l ³ l_пред.

При условиях, когда деформации стержня перестают быть упругими, теоретическое решение задачи от определении при критической силы и критического напряжения сильно усложняется. На основе экспериментальных исследований установлена эмпирическая зависимость критического напряжения s_кр от гибкости стержня

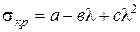(8.9)

(8.9) называется формулой Ясинского – Тетмайера, или эмпирической формулой расчета на устойчивость. Коэффициенты а, в, с в (8.9) имеют размерность напряжения, зависят от свойств материала и определяются опытным путем. Например:

- для стали Ст.2, Ст.3 а=310МПа; в=1,14МПа; С=0.

- для стали Ст.5 а=464МПа; в=3,62МПа; С=0.

- для чугуна а=776МПа; в=12МПа; С=0,053МПа.

- Для дерева (сосна вдоль волокон) а=29,3МПа, в=0,194МПа; С=0

Формула (11.9) применима для стержней, подчиняющихся условию 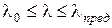, где l₀ – гибкость стержня при s=s_t.