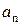Понятия динамической и ударной нагрузки. Учет сил инерции. Продольный удар

Все основные расчетные формулы сопротивления материалов, используемые для проверки прочности, определения размеров поперечных сечений стержней, подбора материала, выявления допустимой нагрузки, были выведены при предположении статического действия внешних сил. Статическое действие сил предполагает изменение их величин настолько медленным, что возникающие ускорения элементов конструкций пренебрежимо малы. Однако во многих случаях действие внешних сил на элементы конструкции сопровождается значительным изменением скорости движения.

Внешние силы, вызывающие ускоренное или замедленное движение элементов конструкции, называются динамическими.

Напряжения, деформации и перемещения, возникающие при динамическом действии сил, также называются динамическими.

Во многих задачах динамические напряжения и деформации можно выразить через статические напряжения и деформации, если ввести дополнительный безразмерный коэффициент, называемый динамическим коэффициентом- k_дин:

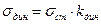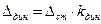, (9.1)

Значение динамического коэффициента k_дин находится в зависимости от условий задачи.

Динамические задачи можно разделить на 2 типа:

1) действие внешних сил таково, что известен закон движения или кинематические параметры движения

2) действие внешних сил продолжается очень малый промежуток времени. Такие силы называются ударными.

Задачи, в которых следует учитывать силы инерции, можно решать в следующей последовательности:

- выявить внешние статические нагрузки, действующие на стержень;

- определить ускорения элементов стержня;

- определить силы инерции элементов стержня;

- определить реакции связей, обусловленные действующими внешними силами и силами инерции;

- методом сечений найти ВСФ и выявить вид сопротивления;

- найти напряжение и деформации по формулам, соответствующим типу сопротивления, произвести необходимые расчеты на прочность и жесткость.

1. Учет сил инерции при поступательном ускоренном движении.

Пусть груз Р поднимается равноускоренно с помощью простейшей лебедки, трос лебедки поперечного сечения А, γ -плотность материала троса. Определить напряжение и деформацию троса длиной z( рис 14.1а)

(9.2)

Очевидно, в состоянии покоя 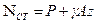. Обозначим (9.3)

С учетом сказанного (9.2) примет вид 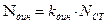(9.4)

Очевидно в случае замедленного движения 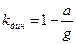. Следовательно, (9.3) можно записать в виде 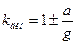с учетом характера движения.

Найдем напряжение s_дин и деформацию Δl_дин :

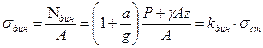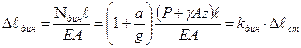
Итак, в случае поступательного равнопеременного движения

,

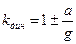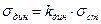2.

qин dФ z dz О а)

Пусть прямой стержень плотностью γ, длиной ℓ вращается равномерно с угловой скоростью ω вокруг оси О. Площадь поперечного сечения-А. Определим напряжение в поперечных сечениях стержня.

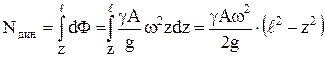. Итак, . Максимальное динамическое напряжение 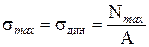, т.е. 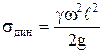(9.7)

3. Напряжение во вращающемся кольце

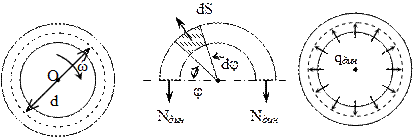
	Пусть кольцо диаметром d плотностью g, вращается равномерно с угловой скоростью w вокруг оси О. Площадь поперечного сечения- А. Определим напряжение в поперечных сечениях кольца.

Разрезав кольцо по горизонтальному диаметру, рассмотрим условие равновесия:

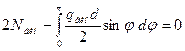. Откуда 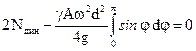. Или

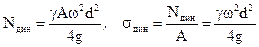(9.8)

4. Напряжения и деформации при ударе

Принимаются следующие предположения:

– материал соударяемых тел подчиняется закону Гука;

– соударяемые тела после удара не разъединяются;

– масса ударяющего тела значительно превышает массу ударяемого тела;

– кинетическая энергия падающего тела полностью переходит в потенциальную энергию деформации ударяемого тела, т.е. потерями энергии, переходящей в теплоту и в энергию колебательного движения соударяющихся тел пренебрегаем.

Рассмотрим продольный сжимающий удар: массивный груз массой Р падает на стержень длиной l, который укорачивается на величину Dl_дин .

задачи, поэтому введя обозначение

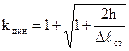(9.11)

Получим Dl_дин = Dl_ст × k_дин. (12)

(11) – динамический коэффициент.

Согласно (11)

– при h = 0, k_дин = 2 (внезапный удар)

– при h >> Dl_ст,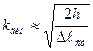

– для уменьшения k_дин, нужно увеличить Dl_ст

Динамические напряжения при ударе

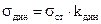(9.13)

где k_дин определяется по формуле (11)

Формула (11) применяется и для поперечного удара (изгиб), и для скручивающего удара (кручение) но вместо Dl_ст используется статический прогиб у_ст , или угол закручивания j_ст .

При расчетах на прочность следует учесть, что допускаемые напряжения при ударе принимают более низкими, чем при действии статических нагрузок.

Результат (11) получен в предпoложении, что удар центральный и не учитывает скорости падения и массу ударяемого стержня.