Тепловая теорема Нернста. Обобщенное уравнение Гиббса - Гельмгольца в дифференциальной форме записи имеет вид (4.42):

Обобщенное уравнение Гиббса - Гельмгольца в дифференциальной форме записи имеет вид (4.42):

.

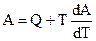После умножения правой и левой его частей на :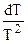

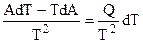
или

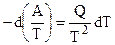. (5.3)

После интегрирования:

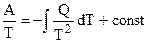
или в более удобной форме записи:

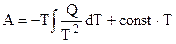. (5.4)

Урвнение (5.4) - интегральная форма записи уравнения Гиббса - Гельмгольца.

Уравнение (5.4) неоднозначно, т. к. в него входит const, значение которой ничем не ограничено. Поэтому в координатном поле “энергия - температура”, вместо одной кривой А = f (T), получается семейство кривых, отличающихся значением const. В то же время зависимость Q=f (T) однозначна и представлена единственной кривой (рис. 5.1).

Для выбора правильной А - кривой достаточно найти одно значение А₁ при какой-либо Т₁, отличной от нуля. Это тот эмпирический путь, условия реализации которого были описаны ранее.

Теорема Нернста позволяет сделать правильный выбор более общим способом. Им было установлено на основании многочисленных экспериментальных данных, что в конденсированных системах Q - кривая и А - кривая сливаются вблизи абсолютного нуля температуры (тепловая теорема Нерста).

Конденсированными называются системы, состоящие из чистых совершенно однородных твердых кристаллических тел, не образующих между собой растворов. Для дальнейшего использования теоремы Нернста ее необходимо выразить в аналитической форме. Слияние двух кривых определяется слиянием их касательных, т. е. равенством пределов их производных при Т 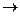0 и значений функций:

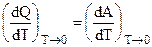и А₀ = Q₀. (5.5)

Для отыскания значения общего предела производных, следует вновь обратиться к уравнению Гиббса - Гельмгольца, переписанному в виде:

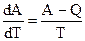. (5.6)

При Т₀ = 0 выражение (5.6) обращается в неопределенность, так как А₀ = Q₀ и 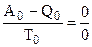. Для ее раскрытия необходимо найти отношение пределов производных от числителя и знаменателя:

.

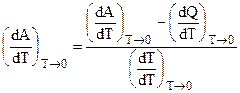Знаменатель этого выражения равен единице, а числитель, согласно (5.5), обращается в ноль. Поэтому:

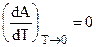(5.7)

и согласно тому же (5.5):

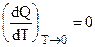(5.8)

Итак, общая касательная кривых Q и А = f (T) параллельна температурной оси (рис. 5.1), что и определяет правильность выбора А = f (T) - кривой.

В дальнейшем теорема Нернста была обоснована более строгим образом, независимо от принципа максимальной работы. Кроме того, было также показано, что жидкости не следует причислять к конденсированным телам, к которым теорема Нернста точно применима.