Расчет абсолютных значений энтропии.

Ранее были получены уравнения, позволяющие вычислять изменение энтропии по известным изменениям параметров системы и известным теплоемкостям.

Формулировка Планка (5.12) позволяет вычислять абсолютное значение энтропии конденсированных веществ, так как в этом случае необходимость выбора условного начала отсчета этой функции отпадает. В самом деле, если рассматриваемое вещество при температуре Т находится в кристаллическом состоянии и в той же модификации, что и при абсолютном нуле, то его энтропия определится следующим образом:

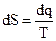, a dq = CdT, тогда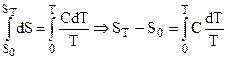

или окончательно

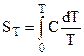, т. к. S₀ = 0.

Если же в интервале (0 - Т) К вещество при температуре Т_Ф.П переходит из одной формы в другую, то следует учесть возрастание энтропии данного фазового перехода согласно уравнению (4.47), которое составит:

,

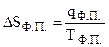где q_Ф.П. - энергетический эффект фазового перехода.

Для примера: рассчитать энтропию газообразного вещества при температуре Т, если при температуре Т_S оно плавится с энергетическим эффектом 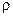, а при температуре Т_Е переходит в газообразное состояние, причем энергетический эффект этого перехода 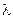. При температуре 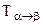происходит полиморфное превращение с энергетическим эффектом .

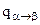Тогда энтропия вещества при температуре Т определится из выражения:

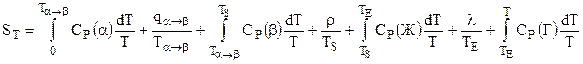, (5.15)

где С_Р( 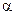) - теплоемкость 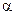- модификации вещества;

С_Р( 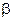) - теплоемкость 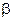- модификации вещества;

С_Р(Ж) - теплоемкость вещества в жидком состоянии;

С_Р(Г) - теплоемкость вещества в газообразном состоянии.

Таким образом можно определить абсолютное значение энтропии веществ в различных состояниях и при любых температурах.

Хотя абсолютное значение энтропии можно определить аналитически с помощью теоретических или эмперических зависимостей С = f (Т), но более надежным является графический метод расчета, тем более что он является и наиболее удобным.

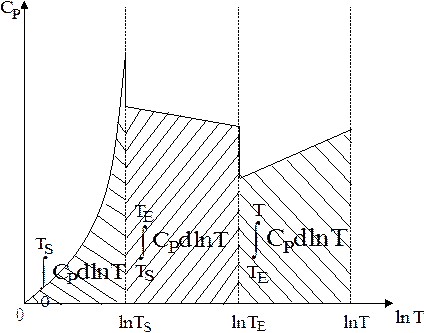
Для этой цели обычно строятся кривые в координатах 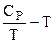или С_Р - lnТ (рис. 5.2).

Площадь, ограниченная кривой, осью абцисс и ординатой при заданной темепературе (Т или lnT) соответствует энтропии при данной температуре за вычетом энтропии фазовых переходов.

Определение абсолютного значения энтропии можно произвести и другими методами. Можно, например, использовать спектральные данные и данные о строении молекул. Полное согласие между результатами определения энтропии этиим двумя методами доказывает справедливость постулата Планка и, в частности, указывает на надежность этих методов.