Розкладання в ряд Тейлора

Команда Symbolics (Символьні обчислення) |Variable(Змінна) | Expand to Series (Розкласти в ряд) виконує розкладання виразу в ряд Тейлора відносно виокремленої змінної з заданим по запиту числом членів ряду n (число визначається по степенях ряду). За замовчуванням приймається n=6. При розкладанні вказується залишкова похибка. На рис. 7.12 представлено фрагмент документа Mathcad з прикладом застосування цієї операції для розкладання функції sin(x)/x.

7.8.6. Розкладання на правильні дроби

Команда Symbolics (Символьні обчислення) |Variable(Змінна) | Convert to Partial Fraction (Розкласти на елементарні дроби) знаходить символьне розкладання виразів, представлених відносно заданої змінної у вигляді суми правильних дробів. На рис. 7.13 представлено фрагмент документа Mathcad з прикладом такого розкладання.

Рис. 7.12. Приклад операції підстановки

Як видно з представлених прикладів, застосування цієї операції в багатьох випадках дає більш довший результат, ніж вихідний вираз. Однак він більш наглядний і сприяє виявленню математичної суті вихідного виразу.

Рис. 7.13. Приклад розкладання на дроби

7.9. Матричні операції

Символьний процесор системи Mathcad забезпечує проведення в символьному вигляді трьох найбільш поширених матричних операцій: транспонування, створення обернених матриць, а також обчислення їх детермінанта. Ці команди в підменю Matrix (Матричні операції) меню Symbolics (Символьні обчислення) позначені так: Transpose (Транспонувати), Invert (Обернути), Determinant(Визначник). Якщо елементи матриці – числа, то відповідні операції виконуються в числовій формі.

Транспонування матриць означає перестановку рядків та стовпців. Вона реалізується командою Transpose. Матриця, що підлягає транспонуванню повинна бути виділена.

Обернені матриці означає створення такої матриці А^-1 , яка при множенні на вихідну матрицю А дає одиничну матрицю, тобто матрицю з діагональними елементами, рівними 1, а решта елементів нульовими. Обернення допустимо для квадратних матриць розмірністю MxN, де N>1 (N – кількість рядків та стовпців матриці). Таку ж розмірність має і обернена матриця.

Рис. 7.14. Приклад матричних операцій

7.10. Інтегральні перетворення

Для виконання інтегральних перетворень служать команди Fourier (Перетворення Фур’є) та Inverse Fourier (Обернене перетворення Фур’є), Laplace (Перетворення Лапласа), Inverse Laplace (Обернене перетворення Лапласа) Z (Z – перетворення), Inverse Z (Обернене Z – перетворення) для Z – перетворення. Ці команди входять Transform (Перетворення) меню Symbolics.

Рис. 7.15. Приклад перетворень Фур’є, Лапласа, Z – перетворення

Для виконання команд перетворення потрібно записати вихідний вираз і виокремити в ньому змінну, відносно якої буде відбуватись перетворення, тільки після цього вказані вище команди стануть доступними.

7.11. Розв’язок рівнянь та систем

В Mathcad рівняння можна розв’язувати не тільки в числовому, але і в символьному вигляді. В робочий документ вводиться рівняння, після чого з допомогою піктограми solve на палітрі Symbolic вводиться однойменна інструкція solve (див. рис. 7.16).

Результат застосування цієї інструкції розглянемо на прикладі розв’язування квадратного рівняння 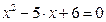. Відповідний фрагмент представлено на рис. 7.17. Праворуч від інструкції solve вказують ту змінну, відносно якої розв’язується рівняння.

Рис. 7.16. Піктограма для розв’язку рівняння

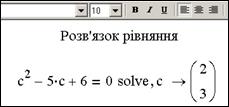
Рис. 7.17. Розв’язок квадратного рівняння

Не слід забувати, що в якості знаку рівності в рівняння вводиться оператор логічної рівності.

Якщо необхідно розв’язати систему рівнянь, то можливі два принципово різних підходи. Один полягає у тому, що рівняння задаються у вигляді елементів вектора. Цей вектор потім вказують ліворуч від інструкції solve, а справа від неї, через кому, перераховують змінні, відносно яких розв’язується система. Результат повертається у вигляді вектора розв’язків. На рис. 7.18 приведений приклад такого способу розв’язку системи рівнянь 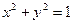та .

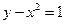Як бачимо з рис. 7.18 знайдено всі розв’язки, в тому числі і комплексні. Альтернативний спосіб розв’язку системи рівнянь полягає у використанні спеціального блока, який починається ключовим словом Given (вводиться з клавіатури) та закінчується функцією Find()або Minerr(). Аргументом функції вказують ті змінні, відносно яких розв’язується система рівнянь. Самі рівняння повинні бути записані в блоці (т.б. між ключовим словом Given та командою пошуку розв’язку Find() або Minerr()). Приклад розв’язку лінійної системи рівнянь таким методом представлений на рис. 7.19.

Рис. 7.18. Розв’язок системи рівнянь, записаний у вигляді вектора

Рис. 7.19. Розв’язок лінійної системи рівнянь

Очевидно, що розв’язок знайдено правильно. Практично так само вирішуються нерівності та системи нерівностей.

7.12. Обчислення нескінченних сум та добутків

На рис. 7.20 наведені приклади обчислення в символьному вигляді суми нескінчених рядів.

Рис. 7.20. Обчислення рядів в символьному вигляді

Практично так само обчислюються нескінчені добутки. Приклади представлено на рис.7.21.

Символьні обчислення суми і добутку вводяться з допомогою піктограми палітри Calculus. На якій є три піктограми для обчислення границь. Піктограми для обчислення правосторонніх та лівосторонніх границь виділено на рис. 7.22.

Рис. 7.21. Обчислення нескінченних добутків