А) б) в)
Рис. 7.22. Піктограми обчислення границь: а) двохсторонньої; б) правостороннього; в) лівостороннього
Обчислення границь
Приклади обчислення границь приведені на рис. 7.23.
Серед інших, там наведені лівосторонні та правосторонні границі. Оскільки функція, для якої визначається границя, є неперервною, всі такі границі співпадають.

Рис. 7.23. Обчислення границь
Питання для самоконтролю
1. Охарактеризуйте коротко команди меню Symbolics?
2. З допомогою яких команд меню Symbolics можна виконувати операції з виокремленими виразами?
3. З допомогою яких команд меню Symbolics можна виконувати операції з виокремленими змінними?
4. З допомогою яких команд меню Symbolics можна виконувати операції з виокремленими матрицями?
5. Назвіть символьні операції інтегральних перетворень.
6. Яке призначення команд підменю Evaluate?
7. Як здійснюється спрощення математичних виразів з допомогою команд меню Symbolics?
8. Як здійснюється диференціювання з допомогою команд менюSymbolics?
9. Як здійснюється інтегрування з допомогою команд меню Symbolics?
10. Як здійснюється розв’язок рівнянь з допомогою команд меню Symbolics?
11. З допомогою яких команд меню Symbolics можна виконувати операції з розкладання в ряд Тейлора та підстановки ?
12. Як здійснюється інтегральні перетворення з допомогою команд меню Symbolics?
ЗАВДАННЯ ДЛЯ ПРАКТИЧНОЇ РОБОТИ №7
Символьні обчислення
Мета роботи.Набути практичні навички роботи з символьним процесором Mathcad.
Вправа 1. Для полінома g(x) (див. табл.1) виконати такі дії:
1. Розкласти на множники.
2. Виконати підстановку виразу x=y+z.
3. Розкласти по ступенях вираз отриманий в п.2.
4. Згорнути вираз отриманий в п.2 по змінній z.
Таблиця 1. Варіанти вправи 1.
| № варіанту | g(x) | № варіанту | g(x) |
| x4 - 2x3 + x2 - 12x + 20 | x4 + x3 - 17x2 - 45x - 100 | ||
| x4 + 6x3 + x2 - 4x - 60 | x4 - 5x3 + x2 - 15x + 50 | ||
| x4 - 14x2 - 40x - 75 | x4 - 4x3 - 2x2 - 20x + 25 | ||
| x4 - x3 + x2 - 11x + 10 | x4 + 5x3 + 7x2 + 7x - 20 | ||
| x4 - x3 - 29x2 - 71x -140 | x4 - 7x3 + 7x2 - 5x + 100 | ||
| x4 + 7x3 + 9x2 + 13x - 30 | x4 + 10x3 +36x2 +70x+ 75 | ||
| x4 + 3x3 - 23x2 - 55x - 150 | x4 + 9x3 + 31x2 + 59x+ 60 | ||
| x4 - 6x3 + 4x2 + 10x + 75 | x4 - 2x3 + 27x - 54 | ||
| x4+16x3 +76x2 +51x-270 | x4+7x3 -7x2 +121x-180 | ||
| x4+7x3 +3x2 -63x-108 | x4+6x3 +6x2 -14x-15 |
Вправа 2. Знайти точки в яких досягається найбільше та найменше значення заданої на відрізку неперервної функції f(x) (див. табл.2). Знайдіть нуль функції на заданому відрізку (розв’яжіть рівняння f(x)=0).
Хід роботи:
1. Побудувати графік функції.
2. Знайти найбільше та найменше значення функції.
3. Розв’язати рівняння f(x)=0, вибравши в якості нульового наближення лівий, а потім правий кінець заданого відрізку.
Таблиця 2 – Варіанти вправи 2.
| № варіанту | f(x) | Відрізок | ||
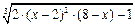
| [0, 6] | |||
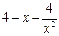
| [1, 4] | |||
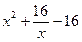
| [1, 4] | |||
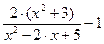
| [-3, 3] | |||
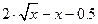
| [0, 4] | |||

| [-1, 5] | |||
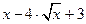
| [1, 9] | |||
| № варіанту | f(x) | Відрізок | ||
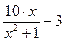
| [0, 3] | |||
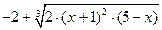
| [-3, 3] | |||

| [2, 4] | |||
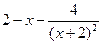
| [-1, 2] | |||
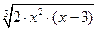
| [-1, 6] | |||
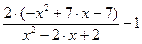
| [1, 4] | |||
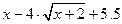
| [-1, 7] | |||

| [1, 5] | |||

| [-4, 2] | |||
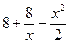
| [-4, -1] | |||
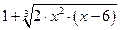
| [-2, 4] | |||
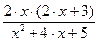
| [-2, 1] | |||
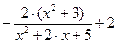
| [-5, 2.8] | |||
Вправа 3. Знайти по визначенню похідну функції f(x) (див. табл.3). Обчислити значення похідної в точці  , враховуючи, що
, враховуючи, що 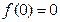 .
.
Хід роботи:
1. Визначити приріст функції в вказаній точці.
2. Обчислити границю відношення приросту функції до приросту аргументу при прямуванні приросту аргументу до 0.
3. Обчислити похідну аналітично.
Таблиця 3 – Варіанти вправи 3.
| № варіанту | f(x) | № варіанту | f(x) |
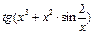
| 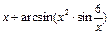
| ||
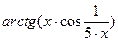
| 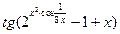
| ||
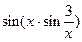
| 
| ||

| 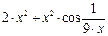
| ||
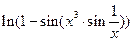
| 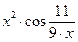
| ||
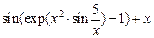
| 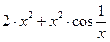
| ||
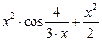
| 
| ||
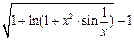
| 
| ||
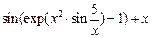
| 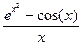
| ||
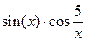
| 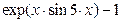
|
Вправа 4. Обчислити визначений інтеграл 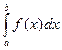 , безпосередньо та з допомогою заміни змінної, згідно варіанту (див. табл.4).
, безпосередньо та з допомогою заміни змінної, згідно варіанту (див. табл.4).
Хід роботи:
1. Обчислити символьно визначений інтеграл функції f(x).
2. Введсти вираз для нової змінної t як функції від x.
3. Обчислити нові границі інтегрування функції f(t) по t.
4. Виразити змінну x через t , розв'язавши рівняння φ(x) - t=0.
5. Знайти символьно похідну f(x) по t.
6. Скопіювати в буфер обміну вираз для f(x) через t та виконати символьно заміну змінної в підінтегральній функції.
7. Спростити підінтегральну функцію.
8. Записати та спростити нову підінтегральну функцію, яка отрималась множенням виразу отриманого в попередньому пункті, на похідну f(x) по t.
9. Обчислити визначений інтеграл, інтегруючи отриману функцію по t на відрізку, знайденому в п.3.
Таблиця 4 – Варіанти вправи 4.
| № варіанту | f(x) | [a, b] | № варіанту | f(x) | [a, b] |
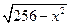
| [0,16] | 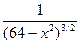
| [0,4 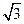 ] ]
| ||
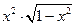
| [0, 1] | 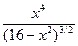
| [0,2 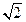 ] ]
| ||

| [0, 5] | 
| [0, 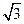 ] ]
| ||
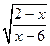
| [3, 5] | 
| [6, 9] | ||

| [0, 2] | 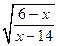
| [8, 12] | ||
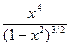
| [0, 2] | 
| [6, 10] | ||
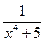
| [0, 4] | 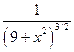
| [0, 3] | ||
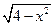
| [0, 2] | 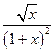
| [1, 5] | ||
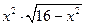
| [0, 4] | 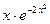
| [0, 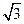 ] ]
| ||
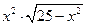
| [0, 5] | 
| [0, 1] |
Вправа 5. Користуючись даними табл.4 обчислити невизначений інтеграл в символьному вигляді.
Глава 8. Програмування в середовищі Mathcad
8.1. Особливості прогорамування
В попередніх розділах розглянуто як у середовищі Mathcad з допомогою вбудованих функцій і операторів виконуються достатньо складні математичні обчислення. Але не дивлячись на всю різноманітність існуючих засобів пакету є задачі, зв’язок яких неможливий без застосування елементів програмування. Програмування в Mathcad не можна назвати повноцінним оскільки не підтримується більшість можливостей, які надають мови високого рівня. Але для великій кількості ситуацій засоби програмування, які надає Mathcad, є цілком достатніми. Програмні блоки просто прикрашають документи і дозволяють користуватись всіма складовими не тільки математично орієнтованої вхідної мови Mathcad, але й класичного програмування.
Для вставки програмного коду в документ у Mathcad маємо панель інструментів Programing (Програмування), яку можна викликати на екран натисканням кнопки Programing Toolbar на панелі Math (Математика).
8.2. Що таке програма?
Основними інструментами роботи в Mathcad є математичні вирази, змінні і функції. Часто записати формулу, яка використовує ту чи іншу внутрішню логіку (наприклад, повернення різних значень в залежності від умови рис.8.1.), в один рядок не вдається. Призначення програмних модулів якраз і полягає у знаходженні змінних, виразів і функцій в декілька рядків, часто з застосуванням специфічних програмних операторів.
Всі Mathcad– програми з точки зору програміста є підпрограмами–функціями, які можуть повертати як результат число, вектор або матрицю. Функції можуть повертати самих себе (рекурсивно задані функції) чи інші підпрограми–функції, визначені перед цим у цьому ж Mathcad–документі.
Приклад:

Рис.8.1. Функція умови як приклад програмного блоку
Не дивлячись на принципову еквівалентність визначення функцій і змінних через вбудовані функції Mathcad або програмні модулі, програмування має суттєві переваги, які часто роблять документ більш простим і наглядним:
· можливість застосування циклів і умовних операторів;
· простота створення функцій і змінних, які вимагають декількох простих кроків;
· можливість створення функцій, які містять закритий для іншого документа код, включно з перевагами використання локальних змінних і обробку особливих ситуацій (помилок).
Програмний модуль позначається тут вертикальною лінією, праворуч від якої послідовно записуються оператори мови програмування.
Дата добавления: 2015-05-19; просмотров: 921;
