Пошук помилок в програмах
Звичайно програми, автори яких не володіють достатніми навичками, навряд чи будуть працювати при першому завантаженні. Очевидно, більшість помилок може бути легко знайдена, але якщо помилка з’явилась вперше, визначити її місцезнаходження не просто. Особливо це стосується великих програм.
У професійних мовах програмування високого рівня помилки, зазвичай, знаходить сама система при виконанні спеціальної процедури, яка називається компіляцією. В Mathcad аналогічної процедури немає, але є інша можливість ефективно визначати синтаксичні помилки в алгоритмі.
Клацнувши правою клавішею мишки над функцією в якій виникла помилка, отримаємо контекстне меню в якому слід вибрати команду розташовану у верхньому рядку – Trace Error (пошук помилки). Далі відкриється спеціальна однойменна панель, яка містить різні пункти для пошуку помилки:
- First (перша). Якщо натиснути цю кнопку, то фрагмент програми, який викликає помилку, зафарбується в червоний колір і виокремиться курсором.
Детальний аналіз виокремленого виразу допоможе знайти помилку, наприклад, відсутність знаку множення. До речі, враховуючи те, що знаки за принципом замовчування в Mathcad не відображаються, візуально знайти таку помилку важко.
- Previous (попередня). Оскільки вплив помилки розповсюджується іноді рівнями (наприклад, при неправильному заданні індекса), виникає необхідність здійснити виправлення у різних місцях програми. Для підняття на рівень вище і використовується ця команда.
- Next (наступна). Команда є ідентичною до попередньої за функціями, але протилежна за напрямом.
- Last (остання). Команда розміщує курсор на останній рівень розповсюдження помилки.
- Close (закрити). Команда призначена для згортання вікна Trace Error.
Питання для самоконтролю
1. Що може бути результатом виконання Mathcad-програми?
2. Як вставити додатковий оператор до вже існуючого програмного блоку?
3. Які логічні операції можна використовувати в середовищі Mathcad?
4. Де зазвичай в Mathcad-програмі використовують оператор otherwise?
5. Чи можна всередині циклу, організованого з допомогою оператора for, присвоювати змінній-лічильнику деяке значення? Відповідь деталізуйте.
6. Коли припиняється повторення тіла циклу при використанні оператора while в Mathcad-програмі?
7. Що отримаємо при використанні оператора break не всередині циклу?
8. Для чого призначено оператор continue?
9. Які засоби перехоплення помилок при виконанні програмного блоку надає Mathcad?
10. В чому зміст в Mathcad рекурсивного задання функції?
ЗАВДАННЯ ДЛЯ ПРАКТИЧНОЇ РОБОТИ №7
Розв’язок диференціальних рівнянь
Мета роботи.Набути практичні навички з розробки програмних блоків у середовищі Mathcad.
Підготувати відповідні програмні блоки для розв’язування у середовищі Mathcad таких завдань:
1. Задано масив А(N,N). Вилучити з цієї матриці стовпчик в якому знаходиться перший парний від’ємний елемент.
2. Задано масив B(М,N). Сформувати масив У(N) із сум від’ємних елементів стовпчиків і впорядкувати його за спаданням.
3. Задано масив А(N,M). Сформувати масив В(М) із сум додатних елементів стовпців матриці А(N,М) і впорядкувати його за зростанням.
4. Задано матрицю С(N,N). Для кожного рядка, що містить від’ємний елемент на головній діагоналі, знайти суму всіх елементів цього рядка і вивести на екран.
5. Задано матрицю В(N,N). В рядках, що містять від’ємний елемент на головній діагоналі, знайти найбільший елемент і вивести його значення та значення його індексів.
6. Задано дві квадратні матриці А(N,N) і В(N,N). Отримати нову матрицю С(N,N) множенням елементів кожного рядка матриці А(N,N) на максимальний елемент відповідного рядка матриці В(N,N).
7. Задана квадратна матриця А(N,N). Отримати одновимірний масив В(N), де В(І) – це мінімальний елемент і-го рядка матриці, крім елемента, що належить головній діагоналі.
8. Задана цілочислова матриця А(N,N). Знайти максимальний елемент стовпця, який містить найменшу суму елементів.
9. Задана матриця А(N,М), яка містить не впорядковані рядки. Знайти максимальні елементи впорядкованих рядків.
10.
11. Відстанню між рядками матриці А(N, M) назвемо суму добутків відповідних елементів рядків. Знайти два рядки з найбільшою відстанню.
13. Задано масив А(N,М). Впорядкувати стовпці за спаданням сум їх елементів.
14. Задано масив В(N,М). Сформувати масив С(N) із сум від’ємних елементів рядків матриці В(N,М), а потім впорядкувати його за зростанням.
15. Задано масив А(N,М). Сформувати масив С(N) із сум додатних елементів стовпчиків і впорядкувати його за спаданням.
16. Задано масив A(N,M). Сформувати масив В(N+M), три елементи якого є добутками елементів стовпців і чотири – добутками елементів рядків масиву A(N,M). Впорядкувати масив В(N+M) за зростанням.
17. Задано масив A(N,M). Впорядкувати стовпці за зростанням добутків їх елементів.
18. В турнірі з баскетболу змагались шість команд. В кожній команді 15 спортсменів. Відомий зріст кожного з них (в сантиметрах). Окремо для кожної команди знайти зріст трьох найвищих баскетболістів.
19. Елемент масиву Аi,j називають сідловою точкою, якщо він є мінімальним в рядку з номером I та максимальним в стовпці з номером j. Знайти сідлові точки.
20.Серед стовпців заданого двовимірного масиву А(N,M) знайти стовпці, які містять тільки непарні елементи. Побудувати нову матрицю X, стовпцями якої є шукані.
Зауваження: Величини N, M, числові значення елементів масивів вибрати самостійно.
Глава 9. Розв’язок диференціальних рівнянь
9.1. Звичайні диференціальні рівняння
Нехай, необхідно знайти розв’язок рівняння
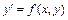 (1)
(1)
з початковою умовою 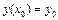 . Така задача називається задачею Коші. Розкладемо задану функцію
. Така задача називається задачею Коші. Розкладемо задану функцію 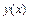 в ряд в околі точки
в ряд в околі точки 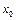 и обмежимось першими двома членами розкладу
и обмежимось першими двома членами розкладу  . Враховуючи рівняння (1) та позначивши
. Враховуючи рівняння (1) та позначивши 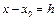 , отримаємо
, отримаємо 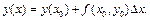 Цю формулу можна застосовувати багаторазово, знаходячи значення функції в все нових та нових точках.
Цю формулу можна застосовувати багаторазово, знаходячи значення функції в все нових та нових точках.
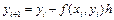 (2)
(2)
Такий метод розв’язку звичайних диференційних рівнянь називається методом Ейлера. Геометрично метод Ейлера значить, що на кожному кроці ми апроксимуємо розв’язок (інтегральну криву) відрізком дотичної, проведеної до графіка розв’язку в початку інтервалу. Точність методу невелика і має порядок h. Говорять, що метод Ейлера – метод першого порядку, тобто його точність зростає лінійно з зменшенням кроку h.
Існують різні модифікації методу Ейлера, що дозволяють збільшити його точність. Всі вони засновані на тому, що похідну, обчислену в початку інтервалу, заміняють на середнє значення похідної на даному інтервалі. Середнє значення похідної можна отримати (звичайно ж тільки наближено) різними способами.
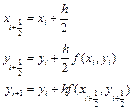 (3)
(3)
Можна, наприклад, оцінити значення похідної в середині інтервалу 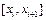 і використовувати його для апроксимації розв’язку на всьому інтервалі.
і використовувати його для апроксимації розв’язку на всьому інтервалі.
Можна також оцінити середнє значення похідної на інтервалі
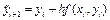
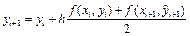 (4)
(4)
Такі модифікації методу Ейлера мають вже точність другого порядку.
Оцінку значення похідної можна покращити, збільшуючи число допоміжних кроків. На практиці найбільш поширеним методом розв’язку звичайних диференційних рівнянь є метод Рунге-Кутти четвертого порядку. Для оцінки значення похідної в цьому методі використовуються чотири допоміжних кроки. Формули метода Рунге-Кутти наступні
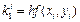
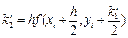
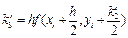
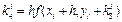
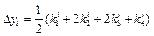
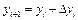
Перераховані методи можна застосовувати і для розв’язку систем диференційних рівнянь. Оскільки багато диференційних рівнянь вищих порядків можуть бути зведені заміною змінних до системи диференційних рівнянь першого порядку, розглянуті методи можуть бути використані і для розв’язку диференційних рівнянь порядку вище першого.
Ще один тип задач, що часто зустрічаються на практиці, – краєві задачі. Нехай, є диференційне рівняння другого порядку 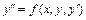 . Розв’язок рівняння необхідно знайти на інтервалі
. Розв’язок рівняння необхідно знайти на інтервалі 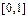 , причому відомо, що
, причому відомо, що 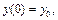
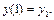 Зрозуміло, що довільний інтервал
Зрозуміло, що довільний інтервал 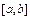 заміною змінних
заміною змінних 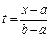 може бути зведений до одиничного. Для розв’язку краєвої задачі звичайно застосовують метод стрільб. Нехай,
може бути зведений до одиничного. Для розв’язку краєвої задачі звичайно застосовують метод стрільб. Нехай, 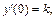 де k – деякий параметр. Для деякого пробного значення k може бути розв’язана задача Коші, наприклад, методом Рунге-Кутти. Отриманий розв’язок буде залежати від значення параметра
де k – деякий параметр. Для деякого пробного значення k може бути розв’язана задача Коші, наприклад, методом Рунге-Кутти. Отриманий розв’язок буде залежати від значення параметра 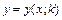 . Необхідно знайти таке значення параметру, щоб виконувалась умова
. Необхідно знайти таке значення параметру, щоб виконувалась умова 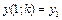 . Фактично ми звели вихідну задачу до задачі розв’язку трансцендентного рівняння з таблично заданою функцією. Якщо знайдені такі значення параметра k1 и k2, що
. Фактично ми звели вихідну задачу до задачі розв’язку трансцендентного рівняння з таблично заданою функцією. Якщо знайдені такі значення параметра k1 и k2, що 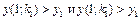 , то подальше уточнення значення параметра можна проводити методом ділення відрізку пополовині.
, то подальше уточнення значення параметра можна проводити методом ділення відрізку пополовині.
9.2. Метод Ейлера для диференціальних рівнянь першого порядку
Розв’яжемо задачу Коші для диференціального рівняння першого порядку 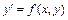 методом Ейлера. Нехай права частина рівняння рівна
методом Ейлера. Нехай права частина рівняння рівна 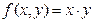 .
.
Задамо границі зміни x: 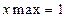 .
.
Задамо кількість точок та величину кроку: 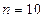 ,
, 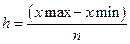
Задамо початкові умови: 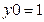 ,
, 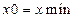 (див. рис.8.1.).
(див. рис.8.1.).
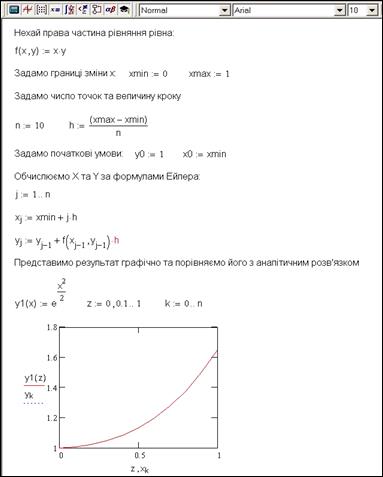
Рис.9.1 Метод Ейлера для диференціальних рівнянь першого порядку
9.3. Розв’язок систем звичайних диференціальних рівнянь
Для розв’язку систем диференціальних рівнянь Mathсad має ряд вбудованих функцій, а саме: rkadapt, Rkadapt,rkfixed.
rkadapt(y,x1,x2,acc,n,F,k,s) повертає матрицю, що містить таблицю значень розв’язку задачі Коші в інтервалі від 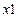 до
до  для системи звичайних диференціальних рівнянь, обчислену методом Рунге–Кутти з змінним кроком і початковими умовами в векторі
для системи звичайних диференціальних рівнянь, обчислену методом Рунге–Кутти з змінним кроком і початковими умовами в векторі 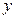 (праві частини системи записані у векторі F, n – число кроків, k – максимальна кількість проміжних точок розв’язку, s – мінімально допустимий інтервал між точками);
(праві частини системи записані у векторі F, n – число кроків, k – максимальна кількість проміжних точок розв’язку, s – мінімально допустимий інтервал між точками);
Rkadapt(y,x1,x2,acc,n,F) – повертає матрицю розв’язків методом Рунге–Кутти з змінним кроком для системи звичайних диференціальних рівнянь з початковими умовами в векторі 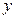 праві частини яких записані в символьному векторі F на інтервалі від
праві частини яких записані в символьному векторі F на інтервалі від 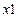 до
до  при фіксованому числі кроків n.
при фіксованому числі кроків n.
rkfixed реалізує метод Рунге–Кутти четвертого порядку з фіксованим кроком. Фактично ця функція призначена для розв’язку систем диференціальних рівнянь першого порядку.
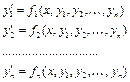
Функція rkfixed(y, x1, x2, n, F) повертає матрицю розв’язків методом Рунге–Кутти системи звичайних диференціальних рівнянь з змінним кроком і початковими умовами в векторі 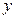 , праві частини яких записані в символьному векторі F на інтервалі від
, праві частини яких записані в символьному векторі F на інтервалі від 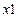 до
до  при фіксованому числі кроків n. Перший стовбець цієї матриці містить точки, в яких отримано розв’язок, а інші стовбці – розв’язки та його перші
при фіксованому числі кроків n. Перший стовбець цієї матриці містить точки, в яких отримано розв’язок, а інші стовбці – розв’язки та його перші 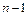 похідні.
похідні.
В якості прикладу розглянемо розв’язок системи двох диференціальних рівнянь методом Рунге–Кутти з фіксованим кроком та адаптивним методом.
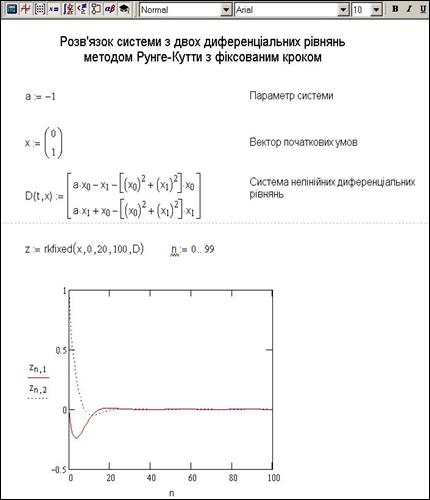
Рис.9.2. Розв’язок системи з двох диференціальних рівнянь методом Рунге–Кутти
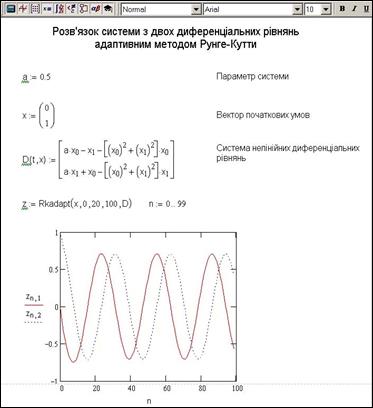
Рис.9.3. Розв’язок системи з двох диференціальних рівнянь адаптивним методом Рунге–Кутти
9.4. Розв’язок диференціальних рівнянь методом Рунге–Кутти
Розв’яжемо ще раз задачу Коші для диференціального рівняння першого порядку  методом Рунге–Кутти. Задамо границі зміни x:
методом Рунге–Кутти. Задамо границі зміни x: 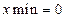 ,
, 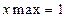 ; число точок всередині інтервалу
; число точок всередині інтервалу 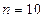 ; початкову умову
; початкову умову 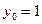 .
.
Зверніть увагу на позначення! Оскільки ми розв’язуємо тільки одне диференціальне рівняння першого порядку, а не систему диференціальних рівнянь, матриця 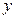 містить тільки один елемент, однак запис
містить тільки один елемент, однак запис 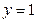 був би неправильний. Необхідно явно вказувати на те, що величина
був би неправильний. Необхідно явно вказувати на те, що величина 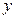 – матриця, тобто необхідно вказувати індекс.
– матриця, тобто необхідно вказувати індекс.
Визначимо тепер матрицю похідних. Ця матриця також складається тільки з одного елемента. Цей елемент з точністю до позначень співпадає з правою частиною вихідного диференціального рівняння: 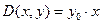 . Розв’язок диференціального рівняння показано на фрагменті рис.9.4.
. Розв’язок диференціального рівняння показано на фрагменті рис.9.4.
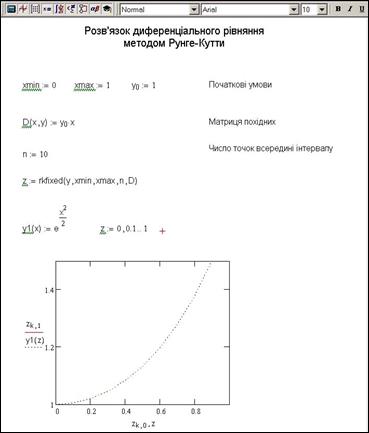
Рис.9.4. Розв’язок диференціального рівняння
9.5. Розв’язок диференціальних рівнянь другого порядку
В якості прикладу розв’яжемо диференціальне рівняння другого порядку
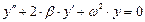
перетворимо до системи з двох диференціальних рівнянь першого порядку
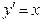
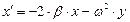
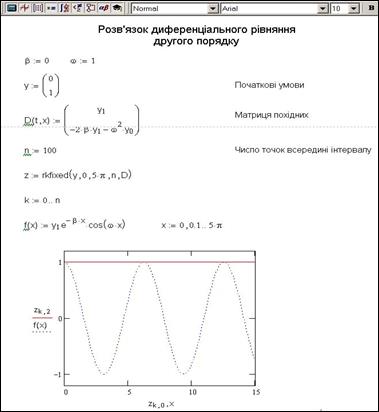
Рис.9.5. Розв’язок диференціального рівняння другого порядку
Примітка: MathCad має ще одну функцію для розв’язку задачі Коші. Це функція Bulstoer, вона має ті ж самі аргументи і повертає розв’язок в тій ж формі, що і функція rkfixed. Але реалізує інший числовий метод – метод Булірша – Штьора. Її слід застосовувати, якщо відомо, що розв’язок є гладкою функцією.
9.6. Розв’язок крєвої задачі
Нехай, необхідно знайти розв’язок диференціального рівняння 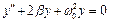 при умові
при умові 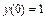 і
і 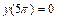 .
.
При значеннях параметрів 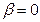 ;
; 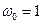 .
.
Для розв’язку краєвої задачі є вбудована функція sbval, що реалізує метод стрільб та дозволяє звести краєву задачу до задачі Коші. Функція sbval має наступні параметри:
· v– вектор, що містить початкові наближення для недостающих початкових умов;
· xmin, xmax– границі інтервалу, на якому шукаються розв’язки;
· D(x,y) – вектор-функція, що містить праві частини системи диференціальних рівнянь першого порядку, що еквівалентні вихідному рівнянню, розмір вектора n співпадає з степеню старшої похідної диференціального рівняння;
· load(xmin,v) – вектор-функція, елементи якої відповідають n значенням функцій на лівій границі інтервалу. Частина цих значень відома, а для частини задані початкові наближення у векторі v. Їх уточнені значення будуть знайдені в процесі обчислення;
· score(xmax,y) – вектор-функція, що має ту ж кількість елементів, що і v. Кожне значення є різницею між початковими значеннями в кінцевій точці інтервалу і відповідній оцінці для розв’язку. Цей вектор показує, на скільки близько знайдений розв’язок до істинного.
Наша задача зводиться до системи двох диференціальних рівнянь першого порядку:
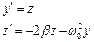
Тому функція D має вигляд рис.8.6.
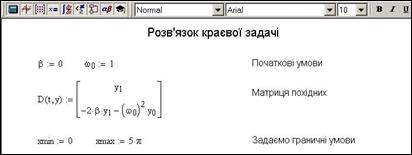
Рис.9.6. Матриця похідних
Задача Коші для диференціального рівняння другого порядку містить дві початкових умови. Нам відомо тільки одну. Початкове наближення для недостающего значення задаємо у векторі v, який в нашому випадку складається тільки з одного елементу. Не дивлячись на це, індекс 0 повинен бути обов’язково вказаний, щоб підкреслити векторний характер цієї величини. На лівій границі інтервалу нам відоме значення y( 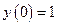 ) і задано початкове наближення для
) і задано початкове наближення для 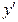 (
(  ).
).
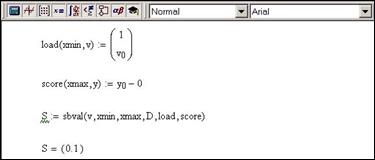
Рис.9.7. Пошук невідомої початкової умови
Це значення записане у v0. Задаємо вектор – функцію load. Її нульовий елемент – початкове значення для  , перший – для
, перший – для  .
.
Тепер, коли нам стало відома початкова умова в задачі Коші, можна скористатись, наприклад, функцією rkfixed.
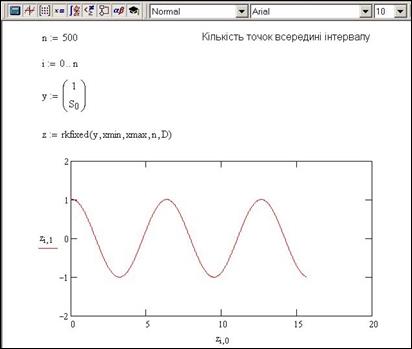
Рис.9.8. Знаходження результатів методом Рунге-Кутти
9.7. Розв’язок звичайних диференціальних рівнянь в Mathcad
Починаючи з версії Mathсad 2000 запропоновано новий спосіб для розв’язку звичайних диференціальних рівнянь, розв’язаних відносно старшої похідної. Для цих цілей служить вже відомий нам блок given разом з функцією odesolve (x, b[кількість кроків]), яка знаходить розв’язок диференціального рівняння при заданих початкових умовах і кінці інтервалу інтегрування b. Диференціальне рівняння разом з початковими або граничними умовами записується в блоці given. Похідні можна позначати як штрихами (Ctrl+F7), так і з допомогою знака похідної  панелі Calculus.
панелі Calculus.
Приклад використання функції для розв’язку задачі Коші приведений нижче.
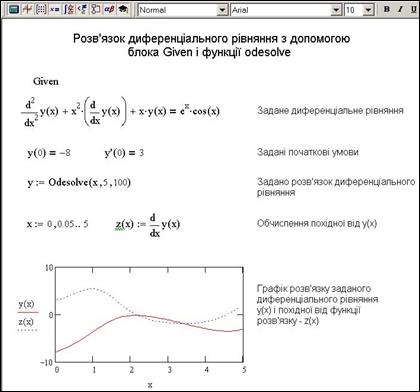
Рис.9.9. Розв’язок диференціального рівняння другого порядку з допомогою функції odesolve
Зверніть увагу, в заданій функції явно заданий аргумент. Функція odesolve має три аргументи. Перший аргумент – незалежна змінна, другий – границя інтервалу, на якому шукається розв’язок, останній аргумент – крок, з яким шукається розв’язок. Останній аргумент можна не вказувати.
Дата добавления: 2015-05-19; просмотров: 1393;
