Преобразование схем замещения

После составления схемы замещения, определения сопротивления всех элементов и приведения сопротивлений к одной ступени трансформации, схема преобразуется к простому виду, показанному на рис. 3.7.

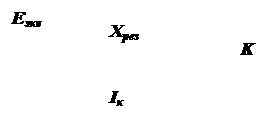
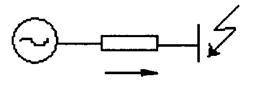
Рис. 3.7. Результирующая схема замещения

При преобразованиях схем в ходе выполнения расчётов нужно учитывать некоторые специфические особенности:

1. Первоочередной задачей расчета КЗ является нахождение тока непосредственно в аварийной ветви или в месте КЗ. Поэтому преобразование схемы нужно вести так, чтобы аварийная ветвь по возможности была сохранена до конца преобразования или, в крайнем случае, участвовала в нем на последних этапах.

С этой целью концы нагрузочных ветвей, ЭДС которых принимаются равными нулю, можно соединять с точкой КЗ, но лучше объединять эти ветви с генераторами в параллельные ветви (рис. 3.8).

2. Для преобразования схем используются методы известные из ТОЭ. Так, последовательные сопротивления непосредственно суммируются, параллельные – суммируются через проводимости и т. д.

Если схема содержит замкнутые контуры, она является сложной, и для преобразования её к простейшему виду необходимо использовать более сложные приёмы. Рассмотрим некоторые из них.

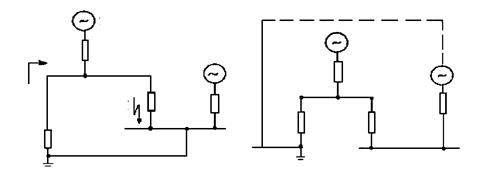
а б

Рис. 3.8. Преобразование схемы:
а – нагрузочная ветвь 3 соединена с точкой КЗ;
б – нагрузочная ветвь соединена с генераторами

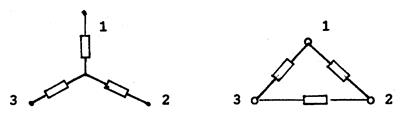
Преобразование треугольника в звезду.

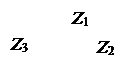
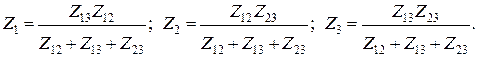(3.32)

Преобразование трехлучевой звезды в треугольник

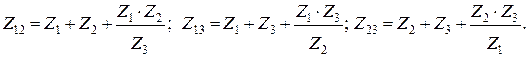(3.33)

3. Замена нескольких источников одним эквивалентным:

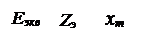
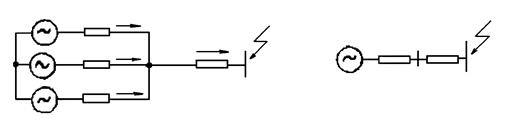
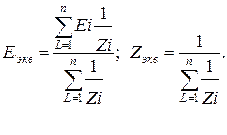(3.34)

При двух ветвях: .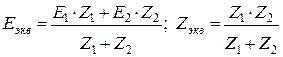

4. Когда металлическое трехфазное КЗ находится в узле с несколькими сходящимися в нем ветвями, этот узел можно разрезать, сохранив на конце каждой образовавшейся ветви такое же КЗ. Далее полученную схему необходимо преобразовать относительно любой из точек КЗ, учитывая другие ветви КЗ как нагрузочные ветви с ЭДС равными нулю (рис. 3.9).

Рис. 3.9. Схема с разрывом точки КЗ

Такой прием эффективен, когда нужно найти ток в одной из ветвей, присоединенных к узлу КЗ.

5. Часто схема замещения бывает симметрична относительно некоторой промежуточной точки. Использование этого обстоятельства позволяет значительно упростить преобразование схемы.

Например, если в представленной на рис. 3.10 а схеме параметры Т1 и Т2, G1 и G2 одинаковы, то потенциалы точек А и В одинаковы, поэтому точки А и В можно либо закоротить, либо разорвать.

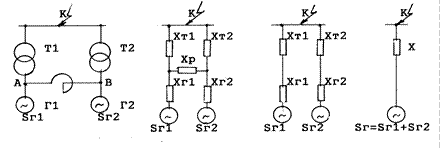
а б в г

Рис. 3.10. Преобразование симметричной схемы

6. Рассмотрим случаи, показанные на рисунке 3.11. Здесь генераторы G₁ и G₂ имеют одинаковые ЭДС, вследствие чего их можно объединить в эквивалентную машину с 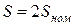. При таком объединении образуется треугольник сопротивлений (x₄, х_6, х₇), который преобразуется в звезду (x₉, х₁₀, х₁₁), как показано на рисунке 3.11 б. В схеме на рисунке 3.11 в определяют сопротивление , .

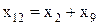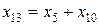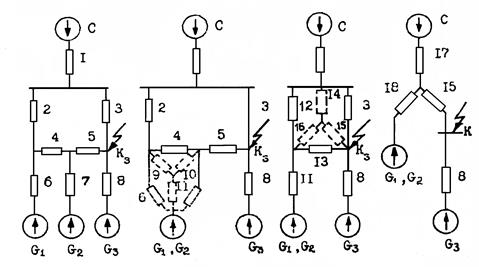
а б в г

Рис. 3.11. Преобразование сложной схемы по методу треугольник-звезда

Получившийся в результате треугольник (x₃, х_12, х₁₃), преобразуется в звезду (x₁₄, х_15, х₁₆). После определения сопротивлений 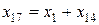и
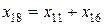получаем окончательную схему, приведённую на рис. 3.11 г.

В ряде случаев преобразования схем замещения ЭЭС упрощается, если трёхлучевую звезду заменить эквивалентным треугольником, затем разрезать его по вершине, где приложены ЭДС. Образовавшиеся параллельные ветви заменяют эквивалентными с такой же ЭДС. Объединение нескольких ветвей иногда полностью не производят и заканчивают двух- трёхлучевой звездой.

Замена двух и более однотипных источников питания одним эквивалентным возможна, если источники питания находятся в практически одинаковых условиях по отношению к точке КЗ, что проверяется по условию

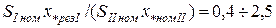, (3.35)

где 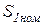, 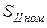– номинальные мощности источников питания;

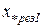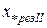, – результирующие сопротивления между соответствующим источником питания и точкой КЗ.

Если расчётное сопротивление ветви между источником питания и точкой КЗ 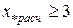, то объединение источников питания допустимо при наличии в схеме ветвей, содержащих источник бесконечной мощности ( 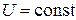) и источник сопротивления ветви 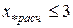, объединять их в один эквивалентный источник не рекомендуется, так как при этом ухудшается точность определения тока КЗ. При упрощении схемы замещения ЭЭС можно пренебречь источником меньшей мощности, если

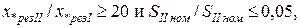(3.36)

где 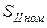– мощность источника питания, меньшего по мощности;

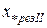– сопротивление цепи между этим источником и точкой КЗ.

Полученные в ходе рассмотренных преобразований эквивалентные ЭДС источников питания и результирующие сопротивления короткозамкнутой цепи являются исходными параметрами для определения токов и напряжений при КЗ.

7. Коэффициенты распределения токов

В практике расчетов токов КЗ часто возникает необходимость в определении взаимных сопротивлений между точкой КЗ и отдельными источниками. Для этой цели используются коэффициенты распределения. Рассмотрим случай, когда два источника связаны с точкой КЗ через общее сопротивление (рис. 3.12).

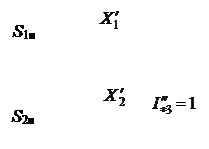
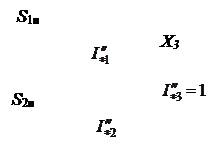
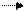
а б

Рис. 3.12. Преобразование схемы с помощью коэффициентов распределения

Для получения схемы рис. 3.12 б необходимо:

А. Определить результирующее сопротивление из схемы, приведённой на рис. 3.12 а:

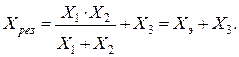(3.37)

Б. Принять относительное значение сверхпереходного тока КЗ в точке К⁽³⁾ равным 1, т. е. 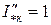, откуда в соответствии с законами Кирхгофа можно записать уравнения:

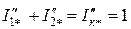; (3.38)

.

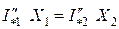В. Совместно решая (3.38), находим:

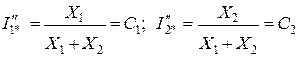, (3.39)

где С₁ и С₂ – коэффициенты распределения, т. е. относительные значения токов КЗ, которыми каждый генератор участвует в питании точки КЗ.

Коэффициенты С₁ и С₂ могут быть определены следующим образом:

.

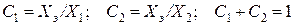Г. Для замены схемы рис. 3.12 а схемой рис. 3.12 б, необходимо соблюсти условия:

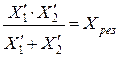; (3.40)

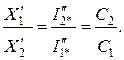
Д. Решая совместно (3.40), получим:

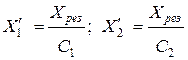. (3.41)

В том случае, если к точке КЗ через общее сопротивление присоединены n источников, расчет производится в следующей последовательности:

А. Определяется эквивалентное и результирующее сопротивления:

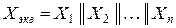; (3.42)

.

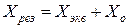Б. Определяются коэффициенты токораспределения:

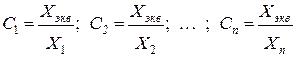, (3.43)

причем .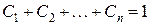

В. Рассчитываются сопротивления новой схемы замещения:

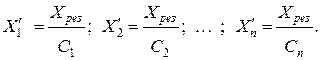(3.44)

8. Трудность преобразования схем замещения в значительной степени определяется выбранным порядком выполнения операций по упрощению схемы. Поэтому при преобразовании схем следует придерживаться такого порядка расчетов и записи результатов, который обеспечивает простую проверку получаемых результатов.

После получения простейшей схемы, содержащей место КЗ и эквивалентную ЭДС за эквивалентным сопротивлением для расчета тока в месте КЗ, а также токи и напряжения в других ветвях схемы (если в этом есть необходимость) определяют, совершая обратный переход – от простейшей схемы к более сложным, вплоть до исходной.

Контрольные вопросы

1. Что понимают под расчетом электромагнитного переходного процесса?

2. Какие задачи решаются благодаря расчёту электромагнитного переходного процесса?

3. Какие условия и основные допущения принимают при расчётах КЗ?

4. Назовите основные этапы расчёта электромагнитных переходных процессов?

5. В чём заключается выбор расчетных условий?

6. Как составляется расчётная схема?

7. Какие параметры элементов СЭС необходимы для расчёта переходных процессов?

8. Как выбираются и пересчитываются базисные условия для различных ступеней напряжения ЭЭС?

9. Зависит ли результат расчёта токов КЗ от выбора базисных условий?

10. На чём основаны точное и приближённое приведения сопротивлений элементов короткозамкнутой цепи (генераторов, трансформаторов, ЛЭП и ректоров) в схемах замещения?

11. Каковы цели расчёта КЗ? Какова последовательность преобразования схем замещения при расчетах?

4. Переходный электромагнитный процесс
при трехфазном КЗ в простейших цепях

4.1. Методы анализа переходных электромагнитных
процессов

Уравнения, описывающие электромагнитные переходные процессы, могут быть записаны в дифференциальной или в операторной форме. Совпадая по существу, они в то же время имеют различные способы решения.

Решение уравнений переходных процессов в дифференциальной форме записи называют классическим методом. В этом случае при малом числе линейных дифференциальных уравнений система с помощью операций дифференцирования и исключения сводится к одному уравнению более высокого порядка, решение которого, как правило, не представляет трудности.

Большое распространение при решении дифференциальных уравнений получил операторный метод решения задач.

Операционное исчисление базируется на специальном интегральном преобразовании функций вещественной переменной, позволяющем заменить операции интегрирования и дифференцирования функций алгебраическими операциями над интегральными преобразованиями (изображениями) этих функций. В результате этого оказывается возможным значительно упростить решение линейных дифференциальных уравнений.