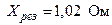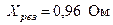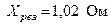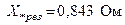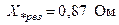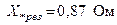Система относительных единиц
Электрические величины могут быть выражены в именованных единицах (I – Амперах (А), U – Вольтах (В), Z – Омах (Ом) и т. д.), процентах (%) и относительных единицах (ОЕ), т. е. в долях от некоторых одноименных величин, называемых в дальнейшем базисными. Относительные единицы широко используются в электротехнических расчетах, так как позволяют значительно упростить выкладки и придают им обобщенный характер.
Определение результирующего сопротивления в относительных единицах возможно только в том случае, если относительные сопротивления всех элементов сети вычислены при одних и тех же базисных условиях.
Например, если в схеме имеются два элемента с параметрами S1, I1, U1, 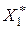 и S2, I2, U2,
и S2, I2, U2, 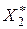 , то просто сложить значения
, то просто сложить значения 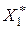 и
и 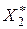 нельзя, так как они определяются при разных условиях. Если же относительные сопротивления этих элементов определить при одной и той же мощности или токе, отнести к одному и тому же напряжению, т. е. подсчитать при одинаковых базисных условиях, то результирующее сопротивление можно определить путем обычных преобразований схемы замещения.
нельзя, так как они определяются при разных условиях. Если же относительные сопротивления этих элементов определить при одной и той же мощности или токе, отнести к одному и тому же напряжению, т. е. подсчитать при одинаковых базисных условиях, то результирующее сопротивление можно определить путем обычных преобразований схемы замещения.
Таким образом, под относительным значением какой-либо величины следует понимать ее отношение к другой одноименной величине, выбранной за единицу измерения.
Следовательно, чтобы выразить отдельные величины в относительных единицах, нужно выбрать те величины, которые должны служить соответственными единицами измерения, т. е. установить базисные единицы или условия.
Пусть за базисный ток и базисное междуфазное напряжение приняты величины Iб и Uб. Тогда базисная мощность трехфазной системы:
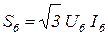 ,(3.20)
,(3.20)
а базисное сопротивление:
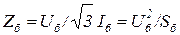 .(3.21)
.(3.21)
Как видно, из четырех базисных единиц Iб, Uб, Sб и Zб две могут быть выбраны произвольно, а две другие получаются из соотношений (3.20, 3.21).
При выбранных базисных условиях относительные значения ЭДС, напряжений, токов, мощностей и сопротивлений будут:
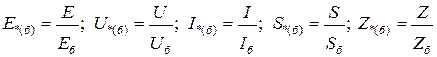 , (3.22)
, (3.22)
где "звездочка" указывает, что величина выражена в относительных единицах, а индекс (б) – что она приведена к базисным условиям.
Поскольку выбор базисных условий произволен, то одна и та же действительная величина может иметь разные численные значения при выражении ее в относительных единицах.
Перепишем из выражений (3.22) сопротивление
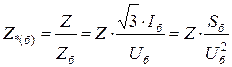 , (3.23)
, (3.23)
где Z – заданное сопротивление, Ом на фазу;
Iб – базисный ток, кА;
Uб – базисное междуфазное напряжение, кВ;
Sб – базисная мощность, МВ·А.
Для различных элементов системы электроснабжения параметры, характеризующие их сопротивления, заданы в разных формах. Так, для воздушных и кабельных ЛЭП задается погонное индуктивное и активное сопротивления на фазу Хо и r0, а также длина L. Поэтому для этих элементов удобнее пользоваться выражением:
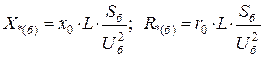 . (3.24)
. (3.24)
Как известно, напряжение КЗ трансформатора задается в процентах от его номинального напряжения. Пренебрегая весьма малой составляющей активного сопротивления обмоток трансформатора, можно считать 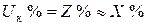 . При этом реактивное сопротивление трансформатора в относительных единицах определяется:
. При этом реактивное сопротивление трансформатора в относительных единицах определяется:
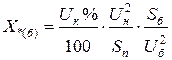 . (3.25)
. (3.25)
Для реактора обычно задается его реактивное сопротивление в процентах Хр %, определенное при номинальных напряжении и токе. Сопротивление реактора, приведенное к базисным условиям, определится:
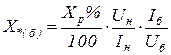 . (3.26)
. (3.26)
Для генераторов и синхронных компенсаторов приводится индуктивное сопротивление 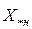 , приведенное к номинальным условиям (табл. 3.2). Сопротивление генератора, приведенное к базисным условиям, будет:
, приведенное к номинальным условиям (табл. 3.2). Сопротивление генератора, приведенное к базисным условиям, будет:
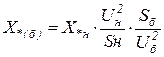 . (3.27)
. (3.27)
При выборе базисных условий следует руководствоваться соображениями, чтобы вычислительная работа была по возможности проще, и порядок числовых значений относительных базисных величин был достаточно удобен для оперирования с ними. Для базисной мощности Sб целесообразно принимать круглые числа (1000, 100, 10 МВ·А) или часто повторяющуюся в заданной схеме номинальную мощность. За Uб рекомендуется принимать Uн или близкое к нему.
Формулы (3.23-3.27) справедливы для схем, содержащих только одну ступень напряжения.
При приведении сопротивлений элементов в относительных единицах к одной ступени трансформации возможно точное или приближенное приведение.
3.5.1. Точное приведение в относительных единицах
Так, если сопротивление Z связано с основной ступенью, для которой выбраны базисные величины Uб и Iб (или Sб), трансформаторами с коэффициентами трансформации К1, К2, ... Кn, то относительная величина его в схеме замещения будет:
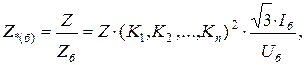 (3.28)
(3.28)
или
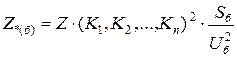 .
.
Этим выражениям можно придать другой вид, введя коэффициенты трансформации в соответствующие базисные величины, т. е.
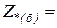
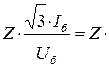
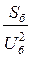 . (3.29)
. (3.29)
где Uб = (1/K1 K2 , ... Kn) Uбв; Iб = (K1K2 , ... Kn) Iбв.
Следовательно, для составления эквивалентной схемы замещения в относительных единицах нужно, прежде всего, на одной из ступеней напряжения заданной схемы выбрать базисные единицы. После этого по формулам:
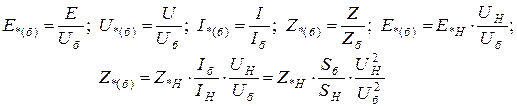 (3.30)
(3.30)
следует подсчитать все величины в относительных единицах при базисных условиях, имея в виду, что в каждом из указанных выражений под Uб, Iб и Zб всегда надо понимать базисное напряжение, ток и сопротивление той ступени трансформации, на которой находятся подлежащие приведению величины.
При такой последовательности приведения магнитосвязнной схемы коэффициенты трансформации промежуточных трансформаторов учтены в базисных единицах каждой ступени напряжения заданной схемы. Этот вариант расчета параметров является более предпочтительным, так как значительно сокращает расчетную часть работы.
3.5.2. Приближенное приведение в относительных единицах
Когда приведение схемы производится приближенно, пересчет к базисным условиям значительно упрощается, если за Uб принимать значение Uср соответствующей ступени. В этом случае можно использовать соотношения:
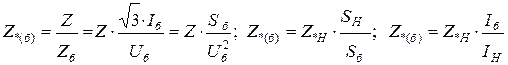 , (3.31)
, (3.31)
помня, что в последнем из них Iб и Iн должны быть отнесены к одной ступени напряжения. Что касается ЭДС и напряжений, то при этих условиях их относительные номинальные и базисные значения совпадают.
Следовательно, при приближенном приведении напряжения в выражениях (3.25-3.28) сокращаются и принимают более простой вид:
– для трансформаторов: 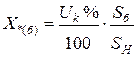 ;
;
– для реакторов: 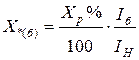 ;
;
– для генераторов, синхронных компенсаторов: 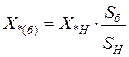 .
.
Выражение для приближенного приведения воздушных и кабельных ЛЭП остается неизменным (3.24), только Uб = Uср.
Формулой приближенного приведения для реакторов следует пользоваться с некоторой осторожностью, так как реактор одного номинального напряжения может быть установлен на стороне меньшего напряжения, и в этом случае необходимо использовать для определения величины его сопротивления формулу (3.26).
Точность расчета не зависит от того, в какой системе единиц выражены параметры схемы замещения.
Если схема замещения составлена в системе относительных единиц, то для получения значений токов и напряжений в именованных единицах нужно полученные относительные величины умножить на соответствующие базисные единицы данной ступени трансформации. Следовательно, при приближенном приведении выражения для определения сопротивлений элементов принимают более простой вид.
Формулы для приведения сопротивлений элементов ЭЭС в относительные единицы при принятых базисных условиях сведены в табл. 3.3.
Таблица 3.3
Формулы для определения реактивных сопротивлений элементов СЭС
| Наименование | Реактивные сопротивления элементов | |||
| Относительные номинальные единиицы | Именованные единицы | Относительные единицы | ||
| Точное приведение | Приближенное приведение | |||
| Синхронный генератор (двигатель, компенсатор) | 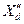 , , 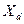
| 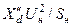
| 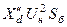
 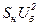
| 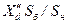
|
| Двухобмоточный трансформатор | 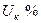
| 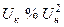
 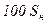
| 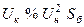
 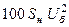
| 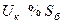
 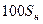
|
| ЛЭП воздушная или кабельная | 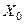 ,Ом/км ,Ом/км
| 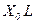
| 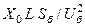
| 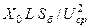
|
| Токоограничивающий реактор | 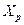 % %
| 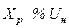
 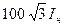
| 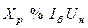
 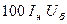
| 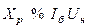
 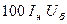
|
| Сдвоенный реактор | 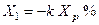 , ,
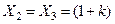 . .
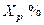 , , 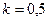 . .
| 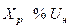
 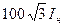
| 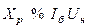
 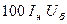
| 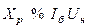
 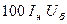
|
| Асинхронный двигатель | 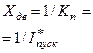
| 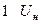
 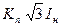
| 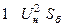
 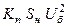
| 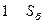
 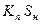
|
| Обобщенная нагрузка | 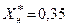
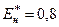
| 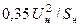
| 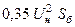
 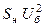
| 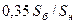
|
Пример 3.1. Для СЭС (рис. 3.6) составить схему замещения для расчёта трехфазного КЗ в точке К и определить результирующее сопротивление короткозамкнутой цепи в именованных и относительных единицах при точном и приближённом приведении.

а
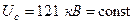 ;
; 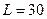 км;
км; 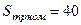 МВ А;
МВ А; 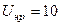 кВ;
кВ;
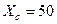 Ом;
Ом; 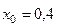 Ом/км;
Ом/км; 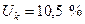 ;
; 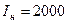 А;
А;
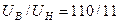 кВ;
кВ; 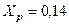 Ом.
Ом.
|
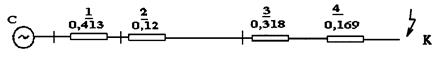
б
|

в
|
|

г
|
|

д
Рис. 3.6. Расчётная схема (а) и схемы замещения с точным приведением
в именованных единицах (б); приближённым приведением в именованных единицах (в); точным приведением в относительных единицах (г);
приближённым приведением в относительных единицах (д)
Решение. Расчёт в именованных единицах с точным приведением параметров к базисным условиям рис. (3.6 б). За базисное напряжение принимаем напряжение ступени, где произошло КЗ, т. е. 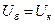 . Тогда
. Тогда
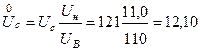 кВ;
кВ;
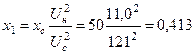 Ом;
Ом;
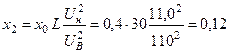 Ом;
Ом;

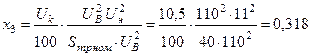 Ом;
Ом;
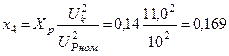 Ом.
Ом.
Результирующее сопротивление цепи КЗ:
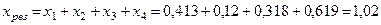 Ом.
Ом.
Расчёт в именованных единицах с приближённым приведением параметров к базисным условиям.
Для рассматриваемой схемы средние напряжения ступеней равны, соответственно, 115 и 10,5 кВ (табл. 2.1). Тогда

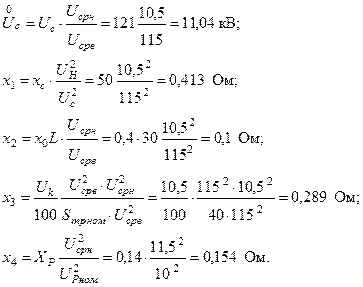
Результирующее сопротивление: 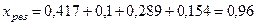 Ом.
Ом.
Расчёт в относительных единицах с точным приведением параметров к базисным условиям. Принимаем за базисную мощность Sб = 100 МВ×А и приводим к ней параметры элементов:
на ступени напряжения, где произошло КЗ 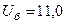 кВ.
кВ.
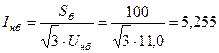 кА;
кА;
на ступени высшего напряжения
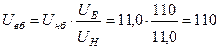 кВ;
кВ;
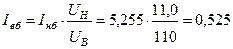 кА.
кА.
Относительное напряжение системы
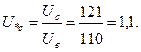
Сопротивления, приведенные к базисным условиям:
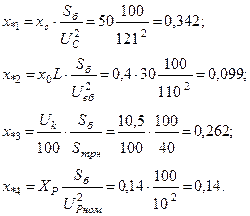
Результирующее сопротивление
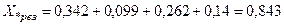 ;
;
определим базисное сопротивление
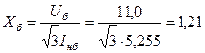 Ом.
Ом.
Величина результирующего сопротивления в именованных единицах
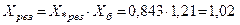 Ом,
Ом,
т. е. величина результирующего сопротивления одинаковая при применении именованных и относительных единиц.
Расчёт в относительных единицах с приближённым приведением параметров.
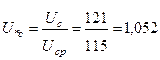 ;
;
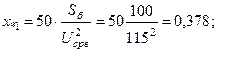
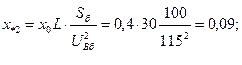
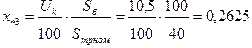 ;
;
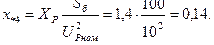
Результирующее сопротивление: 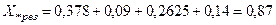 .
.
Базисные ток и сопротивление
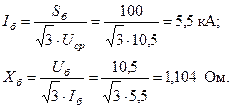
Величина результирующего сопротивления в именованных единицах
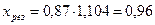 Ом.
Ом.
Дата добавления: 2015-05-19; просмотров: 11990;