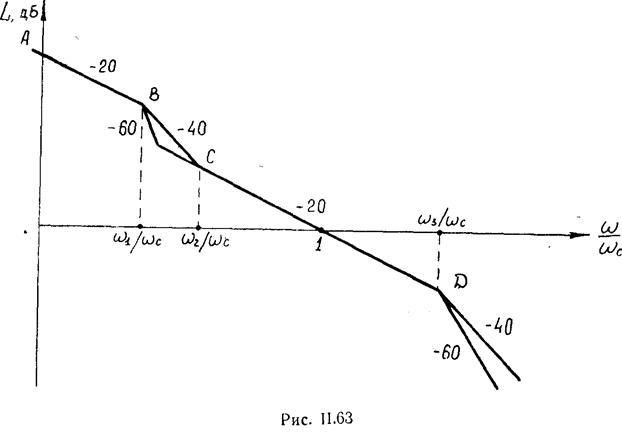
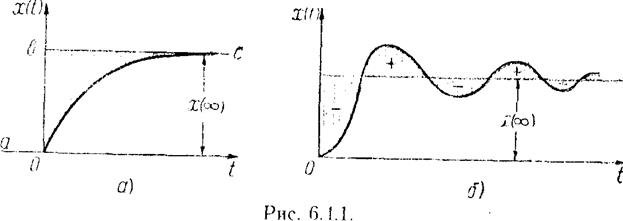
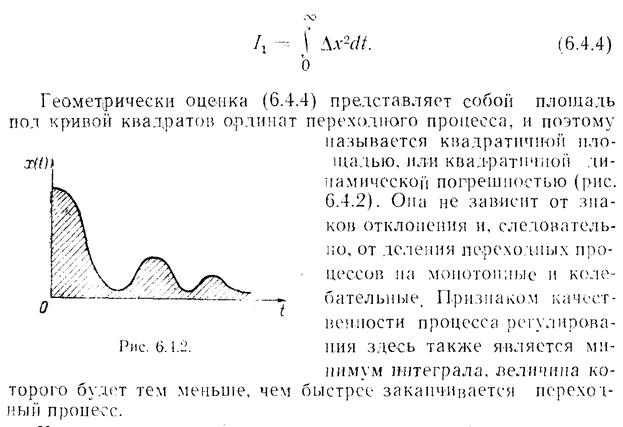
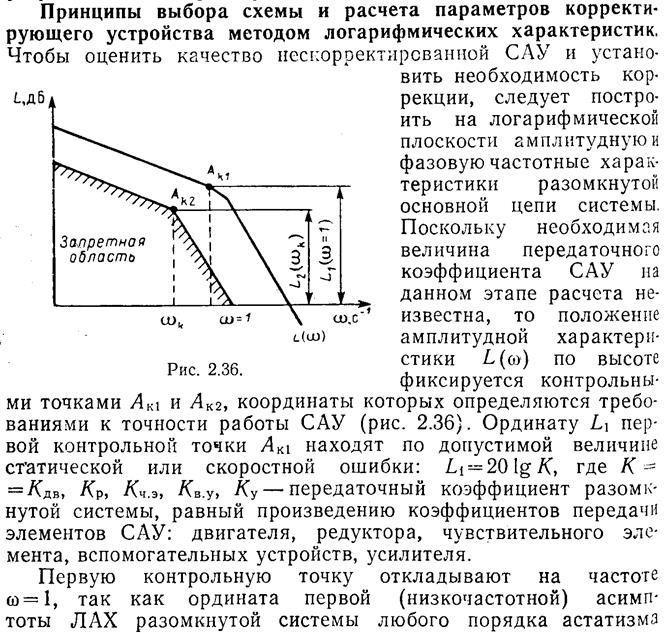
Определение показателей качества переходного процесса по логарифмическим частотным характеристикам.
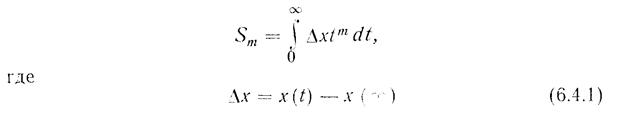
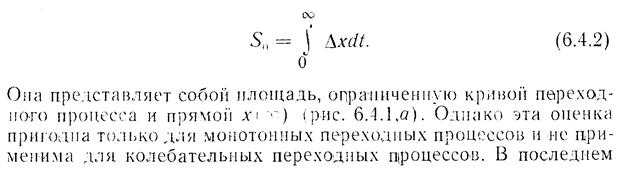
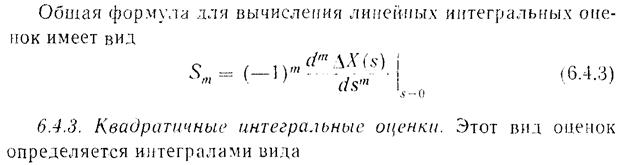
Тема VII: Основы синтеза автоматических систем регулирования.
1. Определение и задачи синтеза САУ.
2. Синтез последовательных корректирующих устройств методом
Солодовникова.
Тема: Математическое описание технологического объекта управления (ТОУ)
1. Структурная схема энергетического канала САУ.
Специфичность систем автоматического регулирования теплоэнергетических установок определяется в основном свойствами и особенностями регулируемого объекта 1.
Под регулируемым объектом в данном случае понимается теплоэнергетическая установка, технологический процесс которой завершается выработкой соответствующего вида энергии. Количественные и качественные показатели энергии обеспечиваются за счет поддержания ее определяющих параметров на заданном уровне, т. е. за счет поддержания работы теплоэнергетической установки на заданном режиме.
С точки зрения теории автоматического регулирования объектом называется элемент, выходная величина которого является регулируемым параметром (величиной) системы автоматического регулирования. Условия работы теплоэнергетической установки, лежащие в основе организации и функционирования системы автоматического регулирования, задаются потребителем. Например, если технологический процесс завершается выработкой электрической энергии, то удовлетворение качественных показателей этого вида энергии обеспечивается постоянством напряжения и частоты переменного тока. Так как частота зависит от угловой скорости, то регулирование по частоте сводится к поддержанию значения угловой скорости на заданном уровне.
Уравнения движения элементов системы автоматического регулирования являются справедливыми только в том случае, когда их составлении выполняется требование энергетического баланса или баланса вещества.
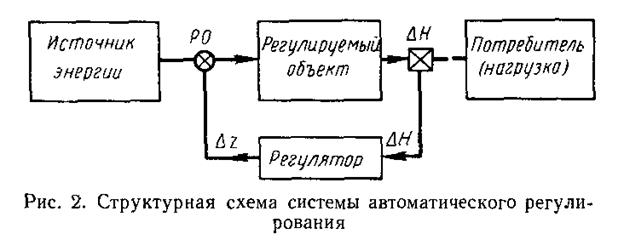
От источника питания в регулируемый объект поступает энергия (масса), которая в регулируемом объекте преобразуется и в виде, удобном для использования, подается потребителю. Поступление энергии или массы в объект можно изменять перестановкой регулирующего органа РО (рис. 2). Если приход энергии в регулируемый объект равен ее отдаче потребителю, то система находится в равновесии (работает на равновесном режиме), а регулируемая величина сохраняет постоянное значение во времени. Например, при уменьшении потребителем расхода энергии в регулируемом объекте накапливается энергия, это приводит к изменению регулируемой величины. Для восстановления равновесия необходимо либо изменить приток энергии перестановкой регулирующего органа, либо изменить ее расход.
2. Задачи статического и динамического анализа САУ.
Анализ работы системы автоматического регулирования и анализ работы ее элементов выполняется для двух возможных состояний: статического и динамического.
Уравнение статики элемента устанавливает зависимость выходной координаты от входных координат, представляющих собой внешние по отношению к элементу возмущения. Уравнение статики позволяет определить связь между выходной координатой и конкретным внешним возмущением при различных равновесных режимах работы.
При статическом анализе системы автоматического регулирования изучают условия обеспечения равновесных (установившихся) состояний, а также выявляют статическую характеристику. Такой анализ позволяет оценить статическую ошибку в поддержании заданного значения регулируемого параметра (степень неравномерности). Выполнение условий работы системы по заданной степени неравномерности и выбору диапазона регулируемых режимов проверяется статическим расчетом. При известном регулируемом объекте статический расчет сопровождается определением параметров элементов автоматического регулятора, которые определяют его конструктивные показатели, обеспечивающие заданную неравномерность и диапазон работы.
Динамический анализ системы автоматического регулирования связан с исследованием ее поведения при нарушении равновесного режима. Предметом исследования в этом случае является процесс изменения регулируемого параметра во времени — так называемый переходный процессcp = cp (t); X = X (t) или т) = ц (t). Нарушение равновесного режима может сопровождаться возвращением системы в исходное состояние, переходом ее в новое равновесное состояние, характеризуемое новым значением регулируемого параметра (в статических системах), или непрерывным удалением от первоначального состояния. В первом и втором случаях система является устойчивой, в третьем — неустойчивой. Поэтому первой задачей динамического анализа работы систем автоматическо го регулирования является оценка системы с точки зрения устойчивости. Вторая задача динамического анализа связана с выявлением качественных показателей переходного процесса (время переходного процесса, максимальное отклонение регулируемой величины от заданного значения, колебательность процесса и т. п.). Третьей задачей анализа является определение влияния параметров элементов, образующих систему автоматического регулирования, на устойчивость и на качественные показатели переходного процесса.
Уравнения движения элементов системы автоматического регулирования, базирующиеся на основе тех же зависимостей (4)—(6), являются линейными дифференциальными уравнениями. Линеаризация связей в элементах системы, обеспечивающая получение линейных дифференциальных уравнений собственно системы, — это основной метод, упрощающий в допустимых пределах решение задач устойчивости и качества переходных процессов.
Нахождение дифференциальных уравнений элементов является основой для получения дифференциального уравнения системы автоматического регулирования. Решение дифференциального уравнения системы регулирования позволяет найти изменение регулируемой величины во времени, т. е. переходный процесс. Знание переходного процесса дает наиболее полное представление о работе системы автоматического регулирования.
Дифференциальные уравнения движения элементов и систем автоматического регулирования записываются в форме, при которой левая часть уравнения содержит выходную величину и ее производные, а правая часть — соответствующие входные возмущения.
3. Классификация объектов тепловой энергетики
по параметру регулирования и их математическое описание.
Если в основу классификации положить параметр регулирования, то объекты регулирования тепловой энергетики можно подразделить на несколько групп, каждая из которых, в качестве регулируемого параметра соответственно имеет угловуюскорость вращения ротора, давление газа или пара в ресивере, уровень жидкости в резервуаре, температуру в камере и т.д.
Каждая из этих групп регулируемых объектов описывается однотипными уравнениями движения.
Первая группа.Равновесный режим работы объектов, отнесенных к данной группе, обеспечивается равенством крутящего момента Мд0, вырабатываемого машиной на равновесном режиме моменту Мс0 потребителя (сопротивления) на этом же режиме!
Уравнение равновесного состояния (уравнение статики) таких объектов имеет вид
Мд0 = Мс0.(34)
Нарушение равновесного состояния, например в связи с изменением нагрузки, приводит к появлению разницы в значениях крутящих моментов машины и потребителя. Отклонение объекта от равновесного состояния вследствие изменения указанных моментов отражается в уравнении динамики объекта. Разница моментов расходуется на ускоренное или замедленное вращение ротора, поэтому
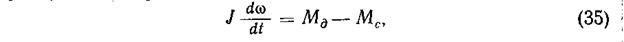
где J — приведенный момент инерции ротора объекта,
принимаемый постоянным; (£> — угловая скорость (выходная координата объекта); Мд и Мс — измененные значения моментов двигателя и потребителя.
Вторая группа.Объекты, относящиеся ко второй группе, представляют собой ресивер определенного объема с коммуникациями подвода и отвода газа.
Уравнение статики таких объектов получает вид
Четвертая группа. Регулируемым объектом этой группы может быть камера, в которой необходимо поддерживать заданное значение температуры. Условие равновесного состояния объекта (уравнение статики) — равенство (на равновесном режиме) подводимого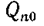 
и отводимого 
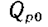тепла
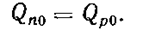
Если равновесное состояние нарушено, то уравнение динамики позволяет определить количество тепла, аккумулируемое в данной камере:
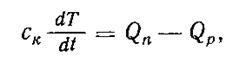
где ск — теплоемкость камеры в ккал/град.
Приведенные выше уравнения динамики регулируемых объектов однотипны и легко подчиняются обобщенной энергетической форме:
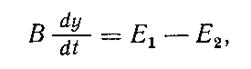
где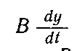 
— аккумулируемая в данном объекте энергия;
В — постоянная объекта; у — регулируемый параметр; Ег и E2 — подводимая и отводимая энергии.
4. Общий вид экспериментальных переходных кривых теплоэнергетических
процессов.
Особенностью реального управления многими инерционными
технологическими процессами, такими как процесс регулирования давления, расхода, уровня, температуры, является апериодичность переходных характеристик.
Увеличение количества емкостей, составляющих регулируемый объект, приводит, очевидно, к соответствующему увеличению порядка дифференциального уравнения, описывающего процесс разгона для регулируемой величины в последней из емкостей при возмущении на входе в объект
Переходный процесс многоемкостного теплового регулируемого объекта за редким исключением описывается дифференциальными уравнениями, характеристические уравнения которых имеют лишь действительные корни. Поэтому процессы разгона в них протекают апериодически, а их кривые разгона являются суммами экспонент (рис. III. 8, кривые 2, 3, 4) и имеют характерную «S-образную» форму. Чем больше составляющих емкостей имеет регулируемый объект при прочих равных условиях, тем более полого идет кривая разгона в начале процесса и тем длительнее его течение (кривые 3 и 4 рис. III. 8). При отсутствии самовыравнивания в регулируемом объекте форма кривых разгона будет несколько иной (рис./III. 9). В этом случае любая из кривых будет уходить в бесконечность, становясь, при достаточном удалении от начала процесса, прямолинейной.
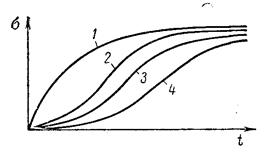
Рис. III. 8. Характеристики разгона многоемкостных объектов при наличии самовыравнивания. Цифры на рисунке соответствуют числу емкостей объекта
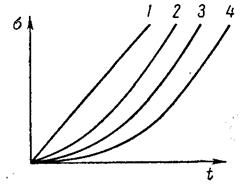
Рис. III. 9. Характеристики разгона многоемкостных объектов в отсутствии самовыравнивания. Цифры на рисунке соответствуют числу емкостей объекта
Общий вид экспериментальных переходных кривых таких процессов характеризуется тремя основамипараметрами: Т, г, V — постоянной времени, временем отставания и скоростью нарастания соответственно, а простейшей обобщенной моделью является модель-
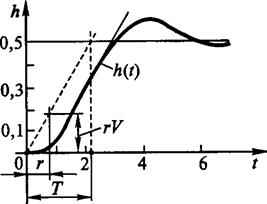
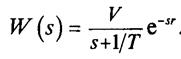
Если к кривой разгона многоемкостного объекта (рис. III. 12) провести касательную в точке ее перегиба (или в бесконечности в случае отсутствия самовыравнивания рис. III. 13), то эта касательная отсечет на оси времени некоторый отрезок, обозначаемый те и называемый емкостным запаздыванием. Из кривых рис. III. 8, III. 9 легко видеть, что емкостное запаздывание при прочих равных условиях тем больше, чем большее число емкостей составляет регулируемый объект. В точке перегиба (или в бесконечности для объектов, лишенных самовыравнивания) скорость изменения регулируемой величины является наибольшей. Следовательно, в соответствии с определением скорости разгона, данной в § 1 и 3, скорость разгона многоемкостного регулируемого объекта может быть определена по углу а наклона касательной в точке перегиба к кривой разгона.
Конечное отклонение регулируемой величины ок определяется степенью самовыравнивания регулируемого объекта и равна ее обратной величине при единичном ступенчатом возмущении. Таким образом, течение процесса разгона многоемкостного регулируемого объекта, а, следовательно, и его кривая разгона приближенно характеризуются тремя величинами — скоростью разгона е, степенью самовыравнивания q и величиной времени емкостного запаздывания те.
В очень большом числе случаев в тепловых регулируемых объектах имеет место так называемое чистое или транспортное запаздывание т0. Оно обусловливается тем, что с момента нанесения возмущения и до того момента, когда регулируемая величина начнет изменяться, должно пройти некоторое время, затрачиваемое на перемещение регулируемой среды от места нанесения возмущения до места измерения регулируемой величины. Это явление хорошо видно на гидравлической модели одноемкостного объекта с запаздыванием (см. рис. II. 20),
При регулировании уровня воды в баке (рис. II. 20) возмущение в виде изменения подачи воды на стороне притока изменяет подачу воды в открытый желоб, по которому вода и подается в бак. Время запаздывания здесь зависит от длины и наклона желоба.
Рис. II. 20. Конструктивная схема запаздывающего звена
Таким образом, типовая характеристика разгона сложного (многоемкостного) теплового регулируемого объекта имеет характерный вид, изображенный на рис. III. 12 и III. 13. Сумма транспортного и емкостного запаздываний
т0 + те = т (III. 11)
называется полным или условным запаздыванием.
Подводя итоги, мы можем отметить следующие основные особенности сложных тепловых регулируемых объектов:
а) процессы разгона в подавляющем большинстве сложных тепловых регулируемых объектов протекают апериодически и, следовательно, их разгонные характеристики монотонны;
б) колебания, проходя через тепловые регулируемые объекты, отстают по фазе от входных колебаний и уменьшаются по своей амплитуде по мере возрастания их частоты;
в) амплитудно-фазовые характеристики тепловых регулируемых объектов в комплексной плоскости представляют собой спирали, закручивающиеся около начала координат, т. е. около точки, соответствующей бесконечно большой частоте колебаний;
г) тепловые регулируемые объекты являются низкочастотными фильтрами и не пропускают практически колебаний, у которых частота равна или больше некоторой частоты среза соер;
д) подавляющее большинство сложных тепловых объектов обладает кроме емкостного также и транспортным запаздыванием.
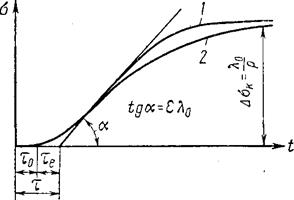
Рис. III. 12..Кривая разгона сложного объекта с самовыравниванием / и аппроксимация ее апериодическим звеном с транспортным запаздыванием т, равным сумме емкостного те и действительного транспортного т0 запаздываний.
Тема: Выбор схем регулирования, типовые алгоритмы регулирования и их
динамические характеристики;
1. Понятие и основные сведения об алгоритме.
При построении систем комплексной автоматизации, особенно систем, включающих цифровые управляющие машины, все больше выявляется недостаточность дифференциальных, разностных и интегральных уравнений как математического аппарата описания процессов управления. Обусловлено это большим количеством логических условий, встречающихся в подобных процессах управления, а также дискретностью многих действий.
Необходим более общий способ описания процессов управления. Таким способом может служить алгоритм.
Термин алгоритм происходит от имени средневекового узбекского математика Аль-Хорезми, который еще в IX в. (825 г.) дал правила выполнения четырех арифметических действий в десятичной системе счисления. Процесс выполнения арифметических действий был назван алгоризмом.
Алгоритм есть совокупность четко определенных правил, процедур или команд, обеспечивающих решение поставленной задачи за конечное число шагов.
Под алгоритмом управления понимают совокупность правил приложения управляющих воздействий к исполнительным элементам объекта управления, обеспечивающих его функционирование с целью решения поставленной перед объектом задачи. Вырабатывает указанные воздействия управляющее устройство на основе уставок и ограничений, введенных оператором (априорная информация), и сигналов датчиков, вводимых обратными связями (текущая информация).
В этом смысле алгоритм управления определяет закон функционирования управляющего устройства, обобщенная функциональная структура которого изображена на рис. 1.2.
Алгоритм — понятие весьма широкое; оно охватывает любую совокупность преобразований и логических условий, действующих в определенном порядке. Например, алгоритмом можно назвать любую инструкцию или предписание, определяющие порядок действия лица в конкретных условиях. Любая передаточная функция системы управленияесть частный вид алгоритма.
2. Способы записи алгоритмов.
Используются следующие способы записи алгоритмов:
• словесный;
• формульный;
• табличный;
• операторный;
• графический;
• язык программирования.
При словесном способе записи содержание последовательных этапов алгоритма описывается в произвольной форме на естественном языке.
Формульный способ основан на строго формализованном аналитическом задании необходимых для исполнения действий.
Табличный способ подразумевает отображение алгоритма в виде таблиц, использующих аппарат реляционного исчисления и алгебру логики для задания подлежащих исполнению взаимных связей между данными, содержащимися в таблице.
Операторный способ базируется на использовании для отображения алгоритма условного набора специальных операторов: арифметических, логических, печати, ввода данных и т, д.; операторы снабжаются индексами и между ними указываются необходимые переходы, а сами индексированные операторы описываются чаще всего в табличной форме.
Графическое отображение алгоритмов в виде блок-схем — весьма наглядный и распространенный способ. Графические символы, отображающие выполняемые процедуры, стандартизованы. Наряду с основными символами используются и вспомогательные, поясняющие процедуры и связи между ними.
Алгоритмы могут быть записаны и в виде команд какого-либо языка программирования. Если это макрокоманды, то алгоритм читаем и пользователем-программистом, и вычислительной машиной, имеющей транслятор с соответствующего языка.
4. Схемы и основные структуры алгоритмов.
Схема алгоритма — графическое представление алгоритма, дополняемое элементами словесной записи. Каждый пункт алгоритма отображается на схеме некоторой геометрической фигурой или блоком. При этом правило выполнения схем алгоритмов регламентирует ГОСТ 19.002—80 «Единая система программной документации» (табл. 1.21).
Блоки на схемах соединяются линиями потоков информации. Основное направление потока информации идет сверху вниз и слева направо (стрелки могут не указываться), снизу вверх и справа налево — стрелка обязательна. Количество входящих линий для блока не ограничено. Выходящая линия — одна, за исключением логического блока.
К основным структурам относятся следующие — линейные, разветвляющиеся, циклические (рис. 1.21).
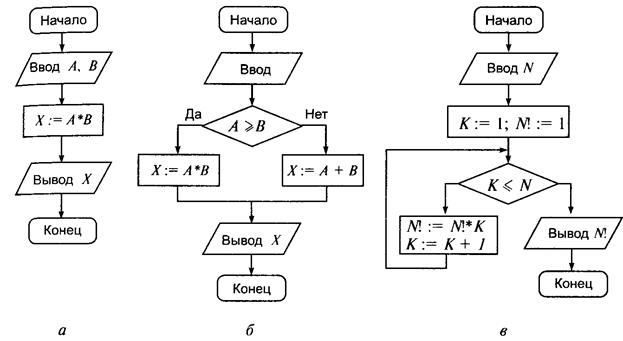
Рис. 1.21. Примеры структур алгоритмов:
a — линейный алгоритм; б — алгоритм с ветвлением; в — алгоритм с циклом
Линейными называются алгоритмы, в которых действия осуществляются последовательно друг за другом. Стандартная блок-схема линейного алгоритма приводится на рис. 1.21, а (вычисление суммы двух чисел — А и В).
Разветвляющимся называется алгоритм, который, в отличие от линейных алгоритмов, содержит условие, в зависимости от истинности или ложности которого выполняется та или иная последовательность команд. Таким образом, команда ветвления состоит из условия и двух последовательностей команд.
Примером может являться разветвляющийся алгоритм, изображенный в виде блок-схемы (рис. 1.21, б). Аргументами этого алгоритма являются две переменные А, В, а результатом — переменная X. Если условие А > В истинно, то выполняется операция X := А х В, в противном случае выполняется Х.= А + В. В результате печатается то значение переменной X, которое она получает при выполнении одной из серий команд.
Циклическим называется алгоритм, в котором некоторая последовательность операций (тело цикла) выполняется многократно. Однако «многократно» не означает «до бесконечности». Организация циклов, никогда не приводящая к остановке в выполнении алгоритма, является нарушением требования его результативности — получения результата за конечное число шагов.
В цикл в качестве базовых входят — блок проверки условия и тело цикла. Перед операцией цикла осуществляется начальное присвоение значений тем переменным, которые используются в теле цикла.
Рассмотрим пример алгоритма вычисления факториала, изображенный на рис. 1.21 (с циклом «ПОКА»). Переменная N получает значение числа, факториал которого вычисляется. Переменной N1, которая в результате выполнения алгоритма должна получить значение факториала, присваивается первоначальное значение 1. Переменной К также присваивается значение 1. Цикл будет выполняться, пока справедливо условие N > К.
4. Декомпозиция алгоритмов управления и сбора
информации в технологической системе.
Общепризнанным направлением в развитии архитектур современных и перспективных АСУ ТП АЭС является распределённость и децентрализация управления технологическими процессами.
Каждая технологическая подсистема или установка в составе системы имеет контур локального управления (регулирования, стабилизации), функцией которого является поддержание некоторого параметра в соответствии с заданным значением. При наступления нового события (выхода некоторого параметра за пределы порогового значения) во многих практически важных ситуациях существует несколько вариантов стабилизации процесса. В простых случаях система управления вычисляет новые значения уставок и сообщает их оператору, который принимает решение об их применении.
В сложных случаях действия оператора не поддаются формализации и их результат зависит от опыта и искусства оператора.
Процесс решения сложной задачи довольно часто сводится к решению нескольких более простых подзадач. Соответственно при разработке сложного алгоритма он может разбиваться на отдельные алгоритмы, которые называются вспомогательными. Каждый такой вспомогательный алгоритм описывает решение какой-либо подзадачи.
Процесс построения алгоритма методом последовательной детализации состоит в следующем. Сначала алгоритм формулируется в «крупных» блоках (командах), которые могут быть непонятны исполнителю (не входят в его систему команд) и записываются как вызовы вспомогательных алгоритмов. Затем происходит детализация, и все вспомогательные алгоритмы подробно расписываются с использованием команд, понятных исполнителю.
Алгоритмы управления и сбора информации в технологически системе целесообразно разделить на семь параллельно работающих групп алгоритмов (автоматов) (рис. 3.3).
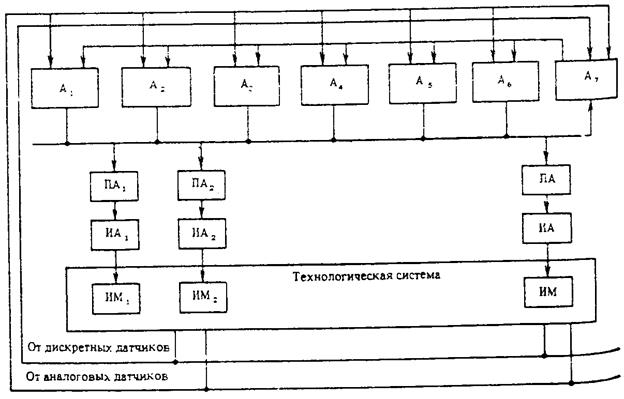
Рис. Схема управления технологической системой.
1. Аварийные защиты А1 описывают ситуации, соответствующие ядерной или пожарной опасности, и действия (команды) на исполнительные механизмы (ИМ), направленные на предотвращение создавшейся ситуации [ос,- (x)hL', в схеме на рис. 3.2].
2 Технологические защиты А2 описывают ситуации, угрожающие —сохранности технологического оборудования, и действия (команды) на исполнительные механизмы, направленные на предотвращение разрушения оборудования [р (х)\- [7;- в схеме на рис. 3.2].
3. Технологические блокировки А3 (одношаговые или многошаговые) определяют действия (операции) над исполнительными механизмами для поддержания технологических параметров (температуры, давления, расхода и т. д.) на заданном уровне или в задании пределах. Другое название алгоритмов А3 - программно-логическое управление.
4. Дистанционное управление от оператора А4 - действия и условия их осуществления над исполнительными механизмами по командам от оператора.
5. Регуляторы А5 - автоматы, осуществляющие поддержание некоторого технологического параметра в соответствии с заданием (управлением) по одному из законов (П, ПИ, ПИД). С точки зрения реализации автоматы А5 - это множество вычислительных процедур, реализующих заданный закон регулирования (П. ПИ, ПИД и т.д.) и условия включения и отключения регулятора.
6. Информационные автоматы формирования событий А6 - это процедуры, задающие правила установления факта события по каждому параметру, исполнительному механизму и алгоритмам управления A1 - A5.
7. Диагностические автоматы А7 - процедуры, осуществляющие функции первичной локальной диагностики исполнительных механизмов, датчиков, локальных процессов.
Каждый автомат А1 - А5 представляет собой набор параллельно непротиворечиво работающих процедур, вырабатывающих управляющие воздействия на исполнительные механизмы. Автоматы А1- А7 работают также параллельно, и детерминизм воздействия обеспечивается на основе арбитража в соответствии с приоритетами в специальных блоках,- приоритетных автоматах {ПА), команды от последних поступают в исполнительные автоматы (ИА), осуществляющие управление элементарными операциями исполнительных механизмов. Последние блоки одинаковы для всех исполнительных механизмов одного типа.
Общая схема управления технологической системой. Каждый томат А1-А5 независимо от других просматривает собственную базу данных, содержащую текущие значения сигналов от датчиков объекта, сигналы от других систем либо команды от оператора, и по ним вычисляет предварительные управляющие воздействия на собственные исполнительные механизмы, которые поступают на приоритетные автоматы, а последние вырабатывают управляющие boj действия или сохраняют предыдущие.
Реализация дистанционного управления в рассматриваемой схеме осуществляется также на уровне управления технологической системой, поэтому помещать его на уровень (блок) операторского интерфейса нецелесообразно.
Процедуры А6 работают одновременно с остальными автоматами осуществляют информационную связь системы управления технологической системой с другими компонентами АСУ ТП, для этого:
устанавливается факт смены состояния любого дискретного входа (выхода) функции и формируется соответствующее сообщение (телеграмма) в систему коммуникации (дискретное событие);
фиксируется изменение любого непрерывного параметра (температуры, давления и т. д.) на заданное с точки зрения точности значение и по этому факту устанавливается параметрическое событие и формируется соответствующая телеграмма в систему коммуникации).
5. Классификация процессов функционирования энергоблока.
Классификация процессов функционирования энергоблока:
стационарные процессы — поддержание параметров, обеспечивающих проектную работу технологического оборудования;
многократные, систематически повторяющиеся технологические процессы — поддержание водно-химического режима, борное регулирование, вывод/ ввод оборудования в соответствии с графиком ремонта и т.п.;
однократные длительные технологические процессы при нормальной эксплуатации — пуск и останов энергоблока;
быстропротекающие процессы с нарушением условий нормальной эксплуатации — отключение части оборудования;
быстропротекающие процессы при возникновении исходных событий проектных аварий.
В зависимости от режима функционирования существенно меняется содержание задач управления. Так, при работе в режимах пуска и останова энергоблока, изменения мощности задачей системы управления является проведение переходных режимов с требуемым качеством и в определенных временных интервалах. Основной задачей при этом является обеспечение безопасного управления энергоблоком.
При работе в базовом режиме задачей системы управления является поддержание требуемого стационарного состояния на неограниченном интервале времени. Основная задача — стабилизация режима и поддержание динамического баланса мощностей в элементах энергоблока.
6. Типовые алгоритмы управления.
Алгоритм управления, его структура и параметры зависят не только от задачи управления, но и от того объекта, которым предстоит управлять. Многообразие объектов управления, не поддающихся типизации, отсутствие единой четкой классификации задач управления затрудняют классификацию алгоритмов управления.
Для упрощенного представления можно выделить среди алгоритмов управления две наиболее обобщенные и укрупненные группы: алгоритмы управления состоянием и сменой состояний. К первым могут быть отнесены алгоритмы поддержания заданного рационального либо предварительно рассчитанного оптимального значения технологического параметра. Они получили название алгоритмов стабилизации или регулирования. Среди них выделяют регулирование по отклонению координаты и регулирование по возмущению. К этой группе могут быть отнесены также алгоритмы статической оптимизации, когда управляющее устройство автоматически осуществляет поиск такого сочетания значений технологических параметров, при котором достигается наилучшее (оптимальное) значение некоторого критерия качества функционирования объекта управления.
Если для достижения оптимального критерия качества необходимо задавать недопустимые значения параметров объекта управления, то формируются предельно допустимые алгоритмы, обеспечивающие наибольшее приближение к оптимуму.
К алгоритмам второй группы следует отнести алгоритмы отработки заданной рациональной или заданной оптимальной траектории -алгоритмы программно-следящего управления. К ним также могут быть отнесены алгоритмы отработки заданной рациональной или оптимальной дискретной последовательности смены технологических операций, образующей технологический цикл.
В отличие от перечисленных алгоритмы динамической оптимизации обеспечивают автоматический выбор оптимальной траектории или ее формирование, коррекцию в процессе отработки в зависимости от меняющихся условий таким образом, чтобы сохранить наилучшее значение критерия качества функционирования.
Наиболее современным и перспективным является оптимальное управление, которое хотя и является обычно наиболее трудно реализуемым, но зато дает наибольший технико-экономический эффект. Решение задач оптимального управления по существу стало реальным в связи с применением в системах автоматизации микропроцессоров и мини-ЭВМ.
7. Типовые алгоритмы регулирования, типовые регуляторы
и их динамические характеристики.
Основными функциями типового регулятора являются усиление сигнала рассогласования и формирование корректирующих сигналов от ошибки, ее производной и интеграла ошибки. Различают несколько разновидностей регуляторов в зависимости от алгоритма формирования корректирующего сигнала: пропорциональный (П-регулятор), интегральный (И-регулятор), пропорционально-интегральный (ПИ-регулятор), пропорционально-дифференциальный (ПД-регулятор), пропорционально-интегрально-дифференциальный (ПИД-регулятор).
Опишем характеристики и параметры настройки типовых регуляторов.
• П-регуляторимеет статическую линейную характеристику, печаточная функция его равна кр. П-регулятор безынерционно реагирует на ступенчатое воздействие.
• И-регуляторимеет передаточную функциювида
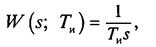
где Т — постоянная времени интегрирования. На входной единичный ступенчатый сигнал И-регулятор реагирует линейным сигналом, причем за время Т выходной сигнал достигает единицы.
• ПИ-регуляторимеет двухпараметрическую передаточную функцию вида
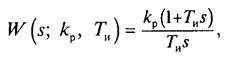
где кр, Ти — коэффициент передачи и время изодрома соответственно. ПИ-регулятор является астатическим регулятором, он совмещает в себе свойства П- и И-регуляторов, его реакция на единичное воздействие представляется мгновенным скачком величины кр и последующим линейно растущим сигналом с наклоном Ти/кр.
• ПД-регуляторимеет передаточную функцию вида
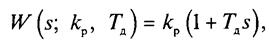
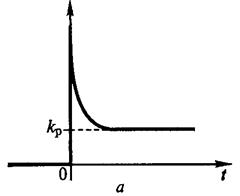
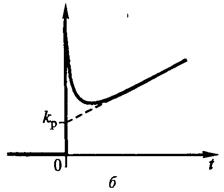
где к , Т — коэффициент передачи и время упреждения соответственно, ПД-регулятор в стационарном режиме ведет себя как пропорциональное звено, но при изменении входного сигнала вырабатывает дополнительную составляющую, соответствующую производной от входного сигнала. Переходная функция регулятора приведена на рис. 5.3, а.
• ПИД-регуляторимеет трехпараметри-ческую передаточную функцию вида
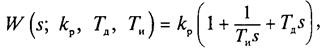
где кр, Г, ТИ — коэффициент передачи, время упреждения и время изодрома соответственно. Структурная модель ПИД-регулятора может быть представлена и в мультипликативной форме
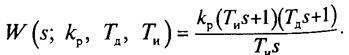
Переходная функция регулятора приведена на рис. 5.3, б. Логарифмическая амплитудная частотная характеристика ПИД-регулятора имеет симметричный вид относительно своей среднечастотной части, наклон в низкочастотной части составляет —20 дБ/дек и 20 дБ/дек в высокочастотной части характеристики, средние частоты подавляются.
8. Выбор схем регулирования типовых теплоэнергетических
процессов и методы настройки типовых регуляторов.
Конкретный вид алгоритмов функционирования отдельных блоков системы управления, структура которой приведена на рис. 3.1, может быть довольно разнообразным.
Рис. 3.1
Особенностью реального управления многими инерционными технологическими процессами, такими как процесс регулирования давления, расхода, уровня, температуры, является апериодичность переходных характеристик. Общий вид экспериментальных переходных кривых таких процессов характеризуется тремя основамипараметрами: Т, г, V — постоянной времени, временем отставания и скоростью нарастаниясоответственно, а простейшей обобщенной моделью является модель
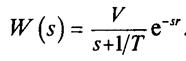
Рис. 5.4
Опыт автоматизации технологических процессов показывает, однако, что на практике для управления такими процессами при Т > (5 + 10)r алгоритмы функционирования регуляторов, как правило, выбираются в виде типового ПИД-алгоритма и его модификаций. Объясняется это тем, что в рамках рассматриваемой структуры системы управления указанные алгоритмы регулирования являются достаточно близкими к оптимальным, если речь идет о выполнении регуляторами свойственных им функций — устранения влияния на процесс управления неконтролируемых случайных возмущений.
Расчет параметров регулятора достаточно прост и практически табулирован, практика настройки системы с ПИД-регулятором доведена до простейших приемов, в чем можно убедиться, используя метод Циглера—Никольса.
В этом методе используют только два параметра r , V, и он тем точнее, чем больше величина третьего параметра Т. Правило настройки регулятора состоит из двух шагов:
• на первом шаге регулятор рассматривают как пропорциональный и увеличивают коэффициент передачи прямого тракта до предельного значения к*, когда система выходит на границу устойчивости и совершает незатухающие колебания с периодом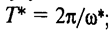 
• на втором шаге определяют параметры регулятора по правилу:
кр = 0,5к*для П-регулятора;
кр = 0,45 к* Тн = 0,83T* для ПИ-регулятора;
кр = 0,6к*, Тн = 0,5 T*, TД = 0,1257* для ПИД-регулятора.
Показатели к*, Т*, по которым определяют параметры настройки регуляторов, находят расчетным путем с использованием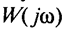 
— частотного годографа Найквиста. В самом деле, предельный коэффициент усиления к* и период Т* = 
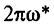однозначно определяются из условия W(jω*) = — 1, когда частотная характеристика разомкнутой части системы проходит через точку —1 на действительной оси.
Параметры регулятора могут быть вычислены и по экспериментально снятой кривой переходного процесса, по которой графически определяют г, Т, V:
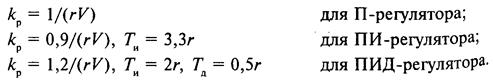
Неудовлетворительная работа системы регулирования, как правило, свидетельствует не о плохой работе ПИД-алгоритма (при условии, конечно, что он настроен оптимально), а о неудовлетворительности информационной структуры системы; для улучшения качества регулирования в этом случае следует попытаться ввести новые добавочные каналы информации о состоянии объекта, т. е. либо перейти к схемам с добавочными регулируемыми величинами, либо ввести компенсирующие сигналы от возмущений.
Напомним также (см. § 1.2), что системы регулирования не предназначены для выполнения функций быстрой отработки относительно больших изменений заданного значения управляемой величины, особенности с учетом проявляющихся в этом случае нелинейных свойств объекта и возможного выхода управляющего органа на ограничения. Для этой цели должны использоваться командные блоки управления, располагаемые на более высоком уровне иерархической структуры системы.
ТЕМА: Алгоритмы отработки дискретной последовательности смены технологических операций, образующих технологический цикл.
Дата добавления: 2015-05-16; просмотров: 2516;