ЛИНЕЙНЫХ СИСТЕМ

Любая САУ характеризуется переходным процессом, который возникает в ней при нарушении состояния равновесия вследствие какого-либо воздействия. Переходный процесс х(t) зависит как от свойств системы, так и от вида возмущающего воздействия. В переходном процессе различают две составляющие:

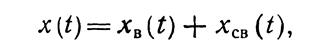
первая из них выражает вынужденные движения, определяемые возмущающим воздействием и свойствами системы; вторая — свободные движения системы, определяемые начальными условиями и свойствами самой системы.

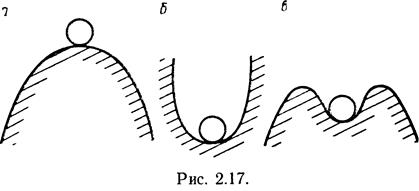
Основной динамической характеристикой САУ является ее устойчивость. Под устойчивостью понимается свойство системы возвращаться к состоянию установившегося равновесия после устранения возмущения, которое вывело ее из этого состояния. Физическую трактовку понятия устойчивости можно пояснить следующим примером. Если шар помещен в верхнюю точку возвышенности (рис. 2.17, я), то система неустойчива, поскольку при малейшем отклонении шара от начального положения он скатится по склону поверхности и не возвратится в исходное положение. Если же шар помещен во впадине (рис 2.17,6), то система устойчива: после отклонения шар обязательно возвратится к первоначальному положению. В обеих ситуациях устойчивость и неустойчивость системы не зависят от величины начальных отклонений шара. Однако возможны случаи, когда система при малых отклонениях будет устойчива, а при больших—неустойчива, например, если шар находится во впадине, а впадина расположена на вершине выпуклой поверхности (рис. 2.17,0). Принято считать, что такая систем; устойчива в малом и неустойчива в большом, поскольку устойчивость связана с величиной начального отклонения.

Система автоматического управления будет устойчива, если в переходном процессе свободная составляющая с течением времени стремится к нулю, т. е. если 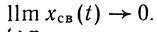. При невыполнении этого условия САУ считается неустойчивой.

Свободное движение системы определяется однородным дифференциальным уравнением

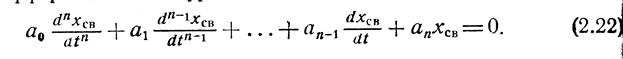
Здесь х_св — свободное движение системы, которое определяет динамическую ошибку; а₀, а_ь .. ., а_п — постоянные коэффициенты, которые определяются параметрами системы. Уравнение (2.22) имеет решение в виде

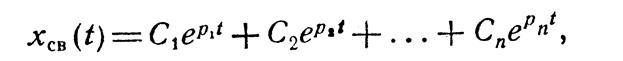
где С_ь С₂, . . ., С_п — постоянные интегрирования, определяемые из начальных условий; р_ь р₂, . .., рп — корни характеристического уравнения системы

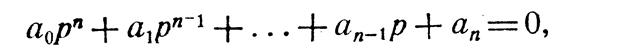(2.24] полученного на основании дифференциального уравнения (2.22).

Если для разомкнутой САУ известна передаточная функция W(P), то для замкнутой системы передаточная функция будет иметь вид

Ф(Р) = W(P)/(1+ W(P))

Откуда, приравни -

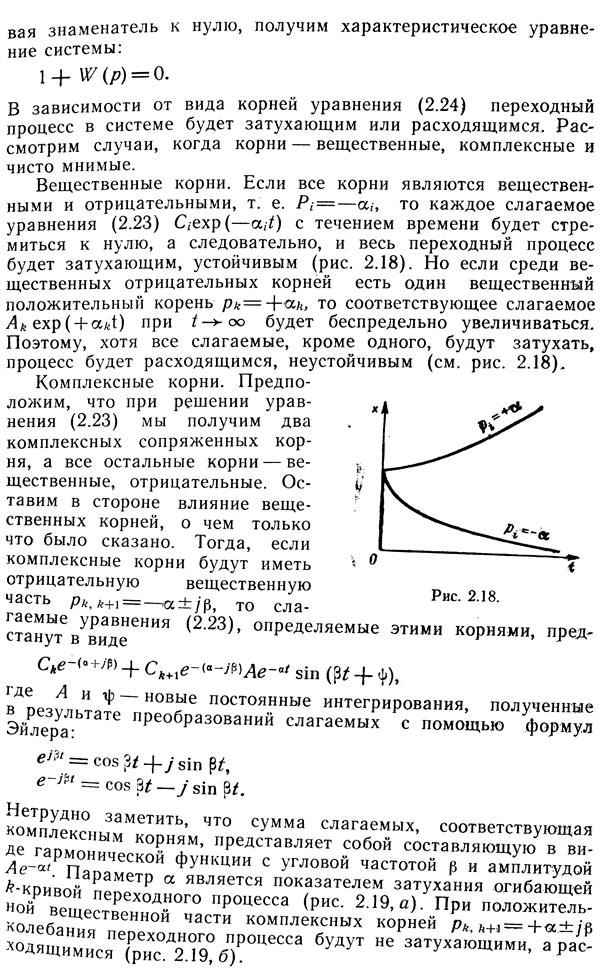
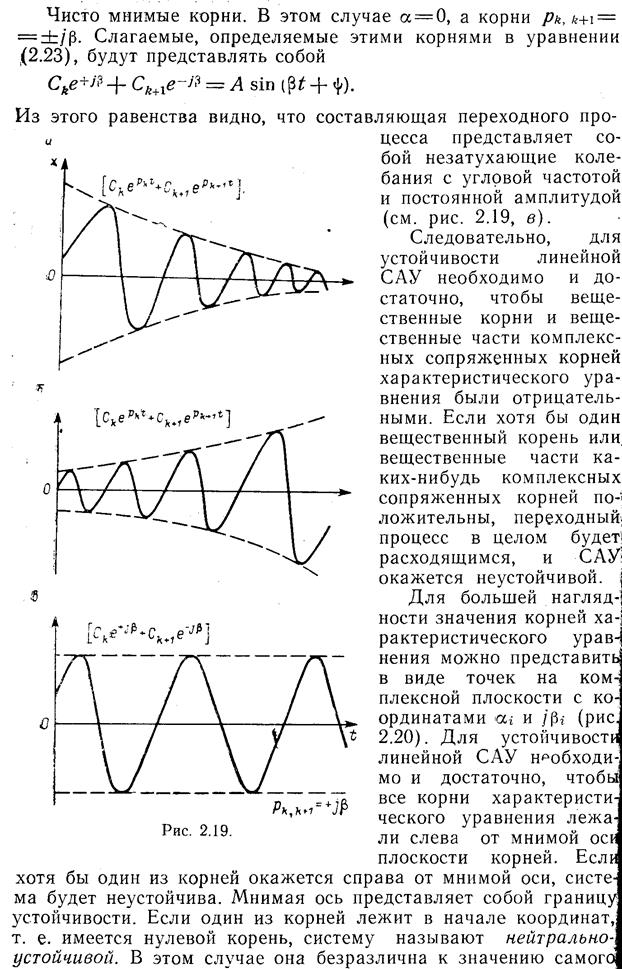
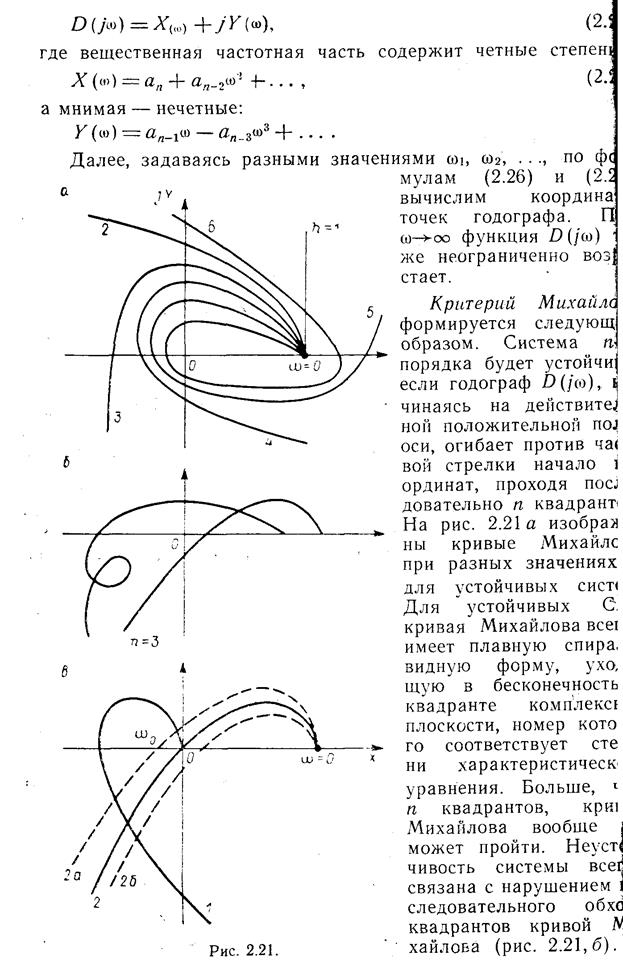
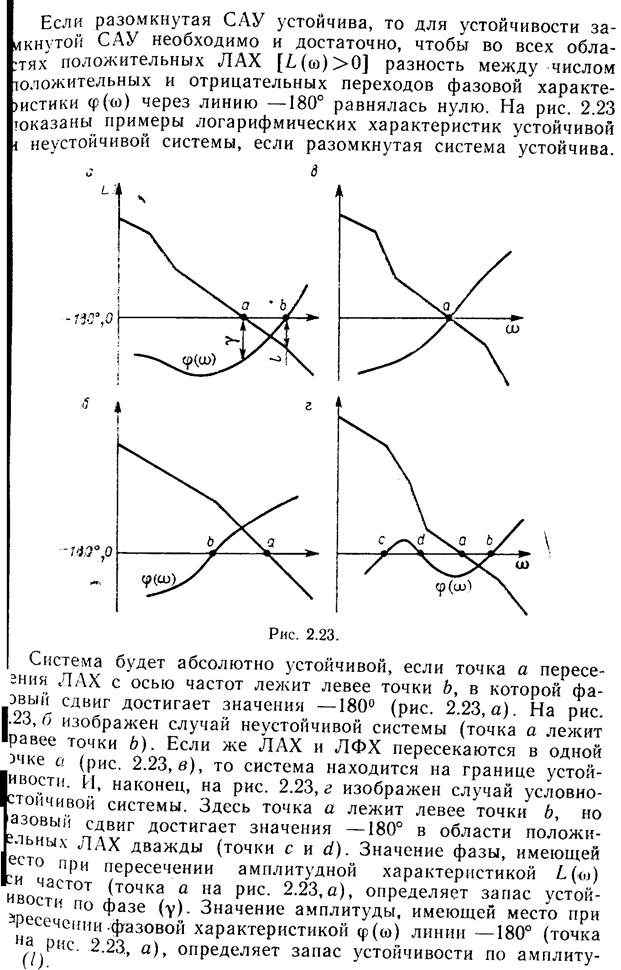
В большинстве случаев для нормальной работы САУ запас устойчивости по фазе составляет около 30°- 60°, а за. по амплитуде—(6-—20) дБ. При оценке устойчивости может считаться достаточным, если отрезок характеристики, пересекающей ось частот с наклоном —20 дБ на декаду, охватывает область частот не менее 0,75 декады.

Исследование устойчивости многоконтурных систем. Большинство реальных САУ имеют не один, а несколько контуров обратной связи, которые улучшают динамические свойства систем. Система, таким образом, становится многоконтурной Управление несколькими параметрами также может быть реализовано многоконтурными системами. Кроме того, с многоконтурными системами сталкиваются при проектировании сложных САУ, состоящих из нескольких взаимодействующих друг с другом следящих систем и систем стабилизации. Анализ устойчивости многоконтурных САУ обычно сложнее, одноконтурных. Одна из основных причин этого — то, что передаточные функции многоконтурных САУ с разомкнутой главной обратной связью не являются произведением простых множителей.

Весьма часто многоконтурные САУ можно упростить, преобразовав их структурные схемы с помощью приемов, рассмотренных ранее. В этом случае исследование устойчивости можно произвести упомянутыми методами. Однако более o6щий метод исследования устойчивости многоконтурной САУ основан на том, что сначала система анализируется известными методами в полностью разомкнутом состоянии, а затем — при последовательном включении каждой из обратных связей, имеющихся в системе.

Необходимо подчеркнуть, что возможны случаи, при которых САУ, устойчивая в своем окончательном рабочем состоянии, может быть неустойчивой, если некоторые из её внутренних обратных связей разомкнуты.

Структурная устойчивость.

Иногда оценить устойчивость САУ можно по ее структуре. Это исключает необходимость составления и решения характеристического уравнения системы. Если система имеет структуру, при которой невозможно обеспечить устойчивость ни каких значениях параметров ее элементов, то она называется структурно-неустойчивой. Примером таких систем могут служить системы, которые имеют два интегрирующих звена.

Предположим, что система, состоящая из одного aпериодического и двух интегрирующих звеньев, имеет передаточную функцию

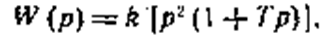
а характеристическое уравнение замкнутой системы

Tp³+p²+k=0

Для этого уравнения необходимое условие устойчивости не вы­полняется ни при каких значениях параметров T и k, следовательно, система будет структурно-неустойчивой.

Структурно-неустойчивую систему можно превратить в устойчивую, только лишь изменив ее структуру, т. е. введением отрицательных обратных связей. Следовательно, в ряде случаев при анализе и синтезе САУ можно заранее отбросить варианты со структурно-неустойчивыми системами. Это особенно существенно при проектировании сложных САУ.

Тема VI: Исследование качества линейных систем.