Основные элементы систем массового обслуживания, их определения, характеристики.

Обслуживаниемназывается процесс удовлетворения какой-либо общественной потребности, например, продажи авиабилетов пассажиру, регистрации пассажира, перевозки груза, заправки горючим, погрузки, разгрузки, хранение и т.д.

Устройства (технические средства, системы, оборудование, обслуживающий персонал), которые непосредственно реализуют функцию обслуживания называются обслуживающими аппаратами (например, касса, регистрационная стойка, бензоколонка, стояночное место, место или ячейка хранения, причал и т.д.).

Обслуживающий аппарат (ОА) образует канал обслуживания. Системы массового обслуживания (СМО) называются много или одноканальными по числу каналов обслуживания.

Общественная потребность выражается в виде заявки на обслуживание. Заявки, поступающие последовательно во времени, образуют поток заявок называемый входным потоком. Например, поток пассажиров, поток воздушных судов, пребывающих в аэропорт, потоки товаров, контейнеров, тары в логистике [7].

Дисциплина обслуживания – порядок обслуживания поступивших заявок. Обслуживанием без приоритета называется обслуживание заявок по мере их поступления.

Поступившая заявка может обслуживаться немедленно или встать в очередь. Место, где заявки ожидают начала обслуживания, называется накопителем (зал пассажиров, часть автомобильной дороги, подъездные пути, склад, область на магнитной ленте, диске ЭВМ).

Если заявка покидает СМО, не получив (или не дождавшись) обслуживания, то говорят, что заявка получила отказ в обслуживании.

Поток заявок, покидающих систему, называется выходным потоком. Выходной поток состоит из потока отказов и потока обслуженных заявок.

Система – это совокупность элементов, связанных между собой и функционирующих совместно для достижения общей цели. СМО – это система, элементами которой являются: входной и выходной потоки, обслуживающие аппараты, очередь, накопитель, дисциплина обслуживания.

Целью СМО является обслуживание потока заявок с наилучшим качеством, эффективностью. Количественные показатели качества обслуживания называются критериями эффективности. Такими критериями являются вероятность отказа в обслуживании, затраты на обслуживание, прибыль, доход, время ожидания обслуживания, их вероятностные характеристики – математическое ожидание, дисперсия.

Время обслуживания заявки, его характеристики. Время обслуживания – основная характеристика обслуживающих аппаратов в теории массового обслуживания. Временем обслуживания называется время ¡, в течении которого обслуживается одна заявка. Время обслуживания - случайная величина. Её полной характеристикой является плотность распределения f(x). Наиболее распространённым законом для описания времени обслуживания является показательный закон:

¦ ( х ) = b е ^-bх , х ³ 0 ,

где b >
- параметр закона распределения.

Средним временем обслуживания называется математическое ожидание времени обслуживания. Эта величина равна:

М ¡ = .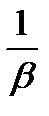

Интенсивностью обслуживания μ называется среднее число заявок, обслуженных одним обслуживающим аппаратом в единицу времени. Интенсивность обслуживания является величиной, обратной среднему времени обслуживания:

μ = 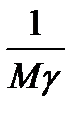= β

Таким образом, параметр β в выражении для плотности распределения равен интенсивности обслуживания.

Входной поток заявок, описание с помощью интервалов между прибытиями. Простейший пуассоновский поток. В теории массового обслуживания входной поток заявок описывается в терминах интервалов между прибытиями:

t₁, t₂, t₃, …, t_к

где t_к – промежутки времени между последовательными заявками (например, - прибытиями пассажиров в аэропорт, воздушных судов, прибывающих на посадку). Величины t₁, t₂,… - являются случайными.

Поток заявок называется потоком с ограниченным последействием, если все величины t_к – независимы между собой. Поток называется простейшим (или пуассоновским), если закон распределения t_к – показательный с плотностью распределения:

¦(х) = l е ^-lх , х ³ 0 ,

где l>0 – параметр, называемый интенсивностью потока. Величина l равна среднему числу заявок (пассажиров, воздушных судов), прибывающих в единицу времени. Интенсивность входного потока, как и интенсивность обслуживания, является величиной, обратной среднему значению интервала между прибытием заявок:

λ = .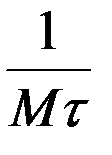

В теории случайных процессов показывается, что для простейшего потока закон распределения числа поступивших заявок на промежутке [ t , t + Dt ] подчиняется закону Пуассона с параметром а = l Dt, т.е. вероятность Р_к того, что появится ровно k заявок вычисляется по формуле:

Р_к = 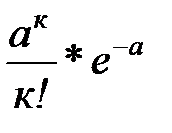; к = 0, 1,…

Пример 1.1. Поток пассажиров, прибывающих в аэропорт для отправления, образует простейший поток с интенсивностью l=2 пассажира в минуту. Найти:

a) Вероятность того, что в течение интервала Dt = 10 минут не прибудет ни одного пассажира;

b) Среднее количество пассажиров, прибывших за 1 час работы аэропорта

Решение. По свойству простейшего потока, число пассажиров, прибывающих в аэропорт, имеет закон распределения Пуассона с параметром:

а = l Dt.

a) В данном случае значение параметра равно:

а = 2 пас/мин * 10 мин = 20 пас.

Вероятность отсутствия пассажиров в течение 10-минутного промежутка равна:

Р₀ = е^-а = е^-20

b) Среднее число пассажиров равно:

а = l Dt = 2 пас / мин * 60 мин = 120 пас

Поток называется стационарным, если закон распределения числа заявок (например, автомобилей или других транспортных средств), поступивших на промежутке [ t, t + Dt ] не зависит от момента времени t.

Если из пуассоновского потока отбросить нечетные заявки, оставив только четные, то получим новый поток. Этот поток называется потоком Эрланга порядка m= 2.

Если оставить заявки с номерами, кратными m= 3 получим поток Эрланга третьего порядка. Поток Эрланга m-го порядка получается путем отбрасывания заявок с номерами, которые не делятся нацело на число m.

Итак, поток Эрланга характеризуется двумя параметрами: l и m.

Пуассоновский поток может рассматриваться как частный случай потока Эрланга при m=1.