МЕРКАТОРСКАЯ ПРОЕКЦИЯ. МЕРИДИОНАЛЬНЫЕ ЧАСТИ

Картографическая сетка меркаторской проекции строится следующим образом. Условный глобус заключается в цилиндр, касательный глобусу по экватору (рис. 2). Меридианы, нанесенные на глобус, распрямляются до тех пор, пока они не коснутся внутренней поверхности цилиндра. При этом меридианы образуют на поверхности цилиндра ряд прямых линий, параллельных между собой. Расстояние между этими .линиями равно расстояниям между меридианами на экваторе глобуса. При распрямлении меридианов параллели растягиваются и становятся равными по длине экватору. На внутренней поверхности цилиндра они обра зуют ряд окружностей. Удлинение параллелей будет тем значительнее, чем ближе они к полюсу.

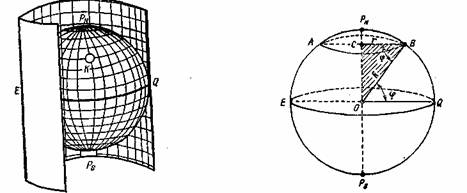
Рис. 2 Рис. 3

Найдем математическую закономерность, которая определяет характер растяжения каждой параллели. Обозначим (рис. 3) радиус параллели АВ, лежащей в широте φ, через r, а радиус Земли — через R. В прямоугольном треугольнике ВОС<СВО = <BOQ= φ. Из этого треугольника получаем

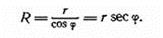
Умножив левую и правую части равенства на 2π, получим в левой части длину экватора, а в правой — длину параллели, умноженную на секанс широты данной параллели,

(*)

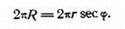Из выражения (*) можно сделать заключение, что любая параллель, удлиняясь до окружности экватора, растягивается пропорционально секансу широты.

Разрежем цилиндр по образующей и развернем его на плоскость. Полученная картографическая сетка удовлетворяет первому требованию к морской карте: так как все меридианы параллельны, то локсодромия изобразится на ней прямой линией.

Однако проекция не является равноугольной, поскольку участки земной поверхности при проектировании будут вытягиваться на ней вдоль параллелей пропорционально секансу φ и, следовательно, не будет сохраняться подобие фигур на местности и на карте, Так, небольшой остров К имеющий круглую форму,изобразится в виде эллипса, вытянутого в широтном направлении (см. рис. 4, а).

Чтобы сделать проекцию равноугольной, необходимо теперь меридианы в каждой точке растянуть так же, как в этой точке растянулась параллель, т. е. пропорционально секансу широты точки. После этого масштаб на каждом небольшом участке карты станет одинаковым как по параллели, так и по меридиану (рис. 4, б).Изображение круглого острова на картографической сетке сохранит свою круглую форму, т. е. проекция будет обладать свойством равноугольности.

Построенная таким методом картографическая проекция, удовлетворяющая обоим требованиям к морской карте, носит название меркаторской.

Масштаб полученной проекции меняется при перемене широты, оставаясь постоянным по направлению параллелей. Поэтому при составлении меркаторской карты главный масштаб указывается по одной из параллелей. За главную параллель может приниматься средняя параллель участка земной поверхности, охватываемого данной картой. Однако при построении карт сравнительно мелкого масштаба за главную, как правило, принимается стандартная параллель данного моря или широтного пояса, даже если она не проходит через карту.

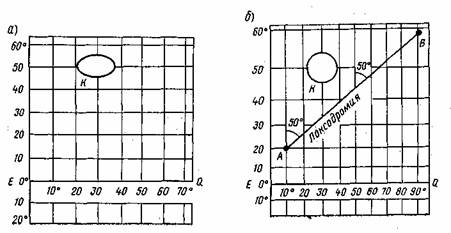
Рис. 4. Построение меркаторской проекции: a — сетка из меридианов и параллелей; б — меркаторска я проекция

Чтобы было удобно измерять расстояния, а также разности широт, боковые рамки меркаторской карты разбивают на участки в 1^/, т. е. на морские мили. Так как при построении карты меридианы вытягивались не равномерно, а пропорционально секансу широты в каждой точке, то морские мили будут изображаться разными по длине участками, увеличивающимися по мере удаления от экватора.

Изображение 1 морской мили на меркаторской карте в данной широте называется меркаторскрй милей.

На экваторе, т. е. в широте 0°, меркаторская миля равна 1 экваториальной миле, в широте 60° — 2 экваториальным Милям (sec 60°= 2), а в широте 80° — 5,8 экваториальным милям (sec 80° = 5,8). При изменении расстояния в какой-либо широте следует пользоваться меркаторскими милями, взятыми с боковой рамки карты в той же широте.

Меридиональной частью (D) называется расстояние на проекции Меркатора по меридиану от экватора до данной параллели, выраженное в экваториальных минутах при масштабе на экваторе, равном единице. Значение и область применения меридиональных частей в картографии и в кораблевождении велики, так как в противоположность переменным численным значениям длины одной минуты меридиана земного эллипсоида меридиональные части выражаются в постоянных величинах, равных длине минуты экватора p_э применяемого эллипсоида. Постоянство единицы меридиональных частей представляет известное удобство при различных вычислениях.
В Картографических таблицах, а также в Мореходных таблицах МТ (табл. 26) приводятся меридиональные части для широт от 0 до 89°59'.

При построении карты в проекции Меркатора всегда указывается параллель, к которой отнесен главный масштаб. Эта параллель называется главной параллелью. Главные параллели установлены для отдельных морей и океанов, их перечень приведен в Картографических таблицах.