Виды картографических проекций и их характеристики
Для выбора наиболее выгодного пути при переходе судна из одного пункта в другой судоводитель пользуется картой.
Картой называют уменьшенное изображение земной поверхности на плоскости, выполненное по определенному способу.
Так как Земля имеет сферическую форму, ее поверхность невозможно изобразить на плоскости без искажений. Если разрезать любую сферическую поверхность на части (по меридианам) и наложить эти части на плоскость, то изображение этой поверхности на ней получилось бы искаженной и с разрывами. В экваториальной части были бы складки, а у полюсов — разрывы.
Для решения навигационных задач пользуются искаженными, плоскими изображениями земной поверхности — картами, в которых искажения обусловлены и соответствуют определенным математическим законам.
Математически определенные условные способы изображения на плоскости всей поверхности шара или его части или эллипсоида вращения с малым сжатием называются картографической проекцией, а принятая при данной картографической проекции система изображения сети меридианов и параллелей — картографической сеткой.
Все существующие картографические проекции могут быть подразделены на классы по двум признакам: по характеру искажений и по способу построения картографической сетки.
По характеру искажений проекции разделяются на равноугольные (или конформные), равновеликие (или эквивалентные) и произвольные.
Равноугольные проекции. На этих проекциях углы не искажаются, т. е. углы на местности между какими-либо направлениями равны углам на карте между теми же направлениями. Бесконечно малые фигуры на карте в силу свойства равноугольности будут подобны тем же фигурам на Земле. Если остров круглой формы в природе, то и на кар- те в равноугольной проекции он изобразится кружком некоторого радиуса. Но линейные же размеры на картах этой проекции будут искажены.
Равновеликие проекции. На этих проекциях сохраняется пропорциональность площадей фигур, т. е. если площадь какого-либо участка на Земле в два раза больше другого, то на проекции изображение первого участка по площади тоже будет в два раза больше изображения второго. Однако в равновеликой проекции не сохраняется подобие фигур. Остров круглой формы будет изображен на проекции в виде равновеликого ему эллипса.
Произвольные проекции. Эти проекции не сохраняют ни подобия фигур, ни равенства площадей, но могут иметь какие-нибудь другие специальные свойства, необходимые для решения на них определенных практических задач. Наибольшее применение в судовождении из карт произвольных проекций получили ортодромические, на которых ортодромии (большие круги шара) изображаются прямыми линиями, а это очень важно при использовании некоторых радионавигационных систем при плавании по дуге большого круга.
Картографическая сетка для каждого класса проекций, в которой изображение меридианов и параллелей имеет наиболее простой вид, называется нормальной сеткой.
По способу построения картографической сетки все проекции делятся на конические, цилиндрические, азимутальные, условные и др.
Конические проекции. Проектирование координатных линий Земли производят по какому-либо из законов на внутреннюю поверхность описанного или секущего конуса, а затем, разрезав конус по образующей, разворачивают его на плоскость.
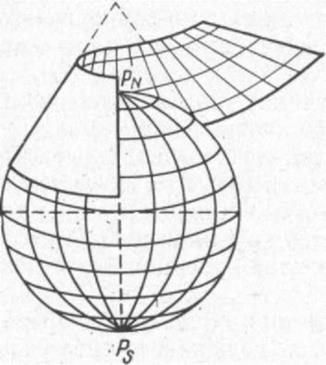
Для получения нормальной прямой конической сетки делают так, чтобы ось конуса совпадала с земной осью PNР S. В этом случае меридианы изображаются прямыми линиями, исходящими из одной точки, а параллели — дугами концентрических окружностей. Если ось конуса располагают под углом к земной оси, то такие сетки называют косыми коническими.
В зависимости от закона, выбранного для построения параллелей, конические проекции могут быть равноугольными, равновеликими и произвольными. Конические проекции применяются для географических карт.
Цилиндрические проекции. Картографическую нормальную сетку получают путем проектирования координатных линий Земли по какому-либо закону на боковую поверхность касательного или секущего цилиндра, ось которого совпадает с осью Земли и последующей развертки по образующей на плоскость.
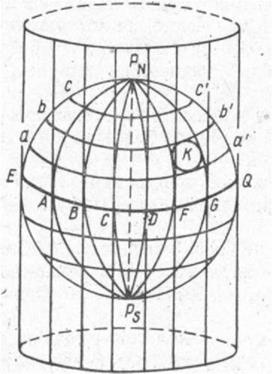
В прямой нормальной проекции сетка получается из взаимно перпендикулярных прямых линий меридианов Л, В, С, D, F, G и параллелей аа',bb',сс При этом без больших искажений будут изображены участки поверхности экваториальных районов (см, окружность К и ее проекцию К на рис. 34), но участки полярных районов в этом случае не могут быть спроектированы.
Если повернуть цилиндр так, чтобы ось его расположилась в плоскости экватора, а поверхность его касалась полюсов, то получается поперечная цилиндрическая проекция (например, поперечная цилиндрическая проекция Гаусса). Если цилиндр поставить под другим углом к оси Земли, то получаются косые картографические сетки. На этих сетках меридианы и параллели изображаются кривыми линиями.
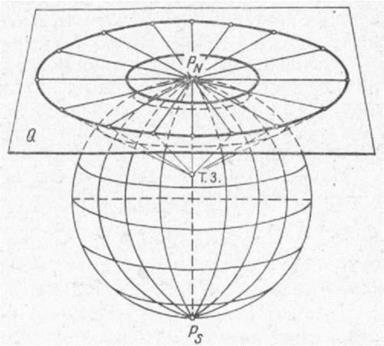
Азимутальные проекции. Нормальную картографическую сетку получают проектированием координатных линий Земли на так называемую картинную плоскость Q — касательную к полюсу Земли. Меридианы нормальной сетки на проекции имеют вид радиальных прямых, исходящих из. центральной точки проекции PN под угла- ми, равными соответствующим углам в натуре, а параллели — концентрическими окружностями с центром в полюсе. Картинную плоскость можно располагать в любой точке земной поверхности, и точку касания называют центральной точкой проекции и принимают за зенит.
Азимутальная проекция зависит от того, какими радиусами проводятся параллели. Подчиняя радиусы той или иной зависимости от широты, получают различные азимутальные проекции, удовлетворяющие условиям либо равноугольности, либо равновеликости.
Основными проекциями, используемыми для составления морских карт, являются:
— равноугольная цилиндрическая проекция Меркатора;
— равноугольная поперечная цилиндрическая проекция Гаусса;
— равноугольная азимутальная, (стереографическая) проекция;
— центральная (гномоническая) проекция;
Дата добавления: 2015-05-13; просмотров: 3658;
