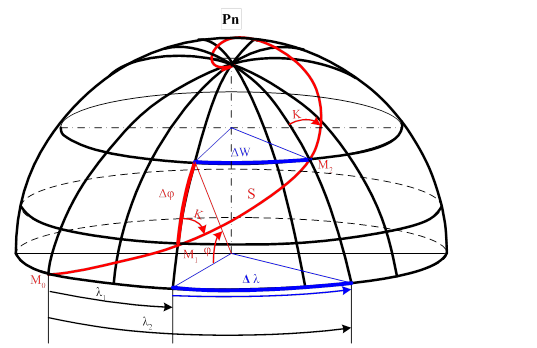
Локсодромия и ортодромия. Ортодромическая поправка.

Кривую на поверхности Земли, пересекающую все мередианы под одним и тем же углом, называют локсодромией, что с греческого переводится как «косой бег».

Расстояние между двумя точками на сфере по локсодромии не является кратчайшим и её применение в мореплавании объясняется исключительным удобством использования компасов.

Уравнение локсодромии для эллипсоида:

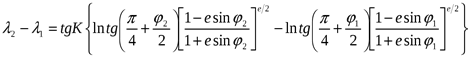
Более краткая запись выглядит так:

,

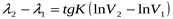Основные свойства локсодромии:

1. 
   Если К = 0 или 180⁰, то tg K = 0. λ₂ - λ₁ = 0 локсодромия совпадает с меридианом, то есть с большим кругом.
2. 
   Если К = 90⁰ или 270⁰, то tg K = беск. φ₂ - φ₁ =0 локсодромия совпадает с параллелью или экватором, то есть образует малый или большой круг на поверхности сферы.
3. 
   При любых других курсах локсодромия спиралеобразно стремится к полюсу, никогда его не достигая.

Рассмотрим изображение локсодромии на карте.

af = D₂-D₁ fb = Δλ

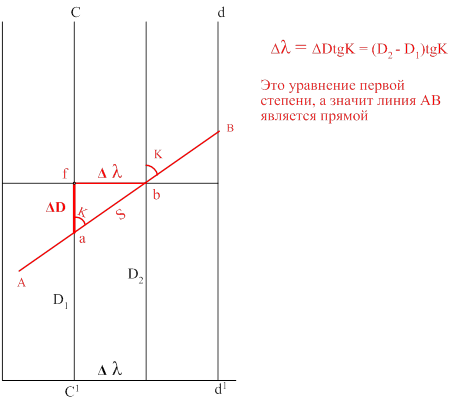
Плавание S определится из рисунка: Sлок = (φ₂ - φ₁)SecK