Моделирование систем массового обслуживания (СМО).

Многие экономические задачи связаны с СМО

, т.е. такими системами, в которых с одной стороны возникают массовые запросы, т.е. требования на выполнение каких-либо услуг, а с другой происходит удовлетворение этих запросов.

СМО включают в себя следующие элементы:

1. источник требований

2. входящий поток требований (очередь)

3. обслуживающие устройства, каналы обслуживания

4. выходящий поток требований

Исследованием таких систем занимается теория массового обслуживания (ТМО). Методами ТМО могут решаться следующие задачи в экономике:

1. в организации торговли эти методы позволяют определить оптимальное количество торговых точек данного профиля, численность продавцов, частоту завоза товаров и др.

2. по складам и базам задача ТМО сводиться к тому, чтобы установить оптимальное соотношение между числом поступающих на базу требований на обслуживание и числом обслуживающих устройств, при котором суммарные расходы на обслуживание и убытки от простоя транспорта были бы минимальными.

ТМО может найти применение и при расчете площади складских помещений, при этом складская площадь рассматривается как обслуживающее устройство, а прибытие транспортных средств под выгрузку как требование.

СМО могут быть классифицированы:

1. В зависимости от условий ожидания начала обслуживания:

- СМО с потерями, т.е. с отказами. В СМО с отказами требования, поступившие в момент, когда все обслуживающие каналы заняты, получают отказ и теряются.

- СМО с ожиданием – требование застав все обслуживающие каналы занятыми становиться в очередь и ожидает пока не освободиться один из обслуживающих каналов.

- СМО допускающие очередь,

- но с ограниченным сроком пребывания каждого требования в ней, называется системой с ограниченным временем ожидания.

2. По числу каналов обслуживания

- Одноканальные

- Многоканальные

3. По месту нахождения источника требований:

- Разомкнутые СМО – источник требований вне системы

- Замкнутые СМО - источник требований находиться в самой системе

Возможны и другие признаки классификации СМО.

Методы и модели ТМО можно разделить на:

- Аналитические

- Имитационные

Аналитические позволяют получить характеристики системы как некоторые функции параметров ее функционирования.

Имитационные основаны на моделировании процессов массового обслуживания на ЭВМ и применяются в том случае если невозможно применение аналитических моделей.

В настоящее время теоретически наиболее разработаны и удобны в практических приложениях методы решения таких задач массового обслуживания, в которых входящий поток требований является простейшим, т.е. Пуассоновским.

Для простого потока частота поступления требований в систему подчиняется закону Пуассона, т.е. вероятность поступления за время t равно k требований задается формулой

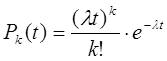
Простейший поток обладает тремя основными свойствами:

1. ординарность потока – практическая невозможность одновременного поступления двух и более требований .

2. стационарность потока – поток, для которого математическое ожидание (средняя величина) числа требований поступающих в систему в единицу времени 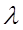не меняется во времени, т.о. вероятность поступления в систему определенного количества в течение заданного промежутка времени 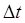зависит от его величины и не зависит от начала его отсчета на оси времени.

3. отсутствие последствия – число требований поступивших в систему до момента t не определяет того, сколько требований поступит в систему за промежуток времени от t до .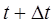

Важная характеристика СМО – это время обслуживания требований в системе. Время обслуживания одного требования является, как правило, случайной величиной, следовательно, может быть описана законом распределения.

Наибольшее распространение получил экспоненциальный закон распределения времени. Функция распределения для этого закона имеет следующий вид:

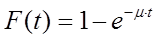
Эта формула определяет то, что вероятность времени обслуживания не превышает некоторой величины t.

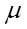- параметр экспоненциального закона распределения, время обслуживания требований в системе.

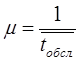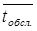, где - среднее время обслуживания

Общая постановка задачи:

Система имеет n обслуживающих каналов, каждый из которых может одновременно обслуживать только одно требование. В систему поступает простейший Пуассоновский поток требований с параметром 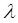, если в момент поступления очередного требования в системе на обслуживании уже находиться не меньше n требований, т.е. все каналы заняты, то это требование становиться в очередь, и ждет начала обслуживания. Время обслуживания каждого требования t – случайная величина , которая подчиняется экспоненциальному закону распределения с параметром .

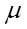СМО с ожиданием разбиваются на две группы:

- Замкнутые

- Разомкнутые