М-метод решения задач линейного программирования.
Трудности, которые возникали при выделении допустимого базиса симплекс-методом, они явились толчком к разработке модификации симплекс-метода называемого м-методом, его называют методом искусственного базиса.
f(x) = d1x1 + d2x2 + d3x3 + … + dnxn + d 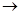 min
min
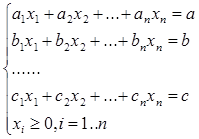
В те уравнения, где нет допустимой базисной переменной, вводят искусственные базисные переменные
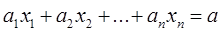
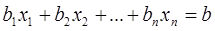
………
В те уравнения, где есть допустимая базисная переменная, мы не вводим искусственные переменные
f(x) = d1x1 + d2x2 + d3x3 + … + dnxn + d + My1 + My2 + My3 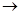 min, где М – очень большое положительное число, т.е. М выбирается столь большим чтобы все встречающиеся по ходу выкладок выражения вида a + bM, с положительным «b» были положительными. Затем составляем расширенную матрицу.
min, где М – очень большое положительное число, т.е. М выбирается столь большим чтобы все встречающиеся по ходу выкладок выражения вида a + bM, с положительным «b» были положительными. Затем составляем расширенную матрицу.
После этого составляется первая симплекс-таблица.
Если при решении М-задачи симплекс-методом, получается симплекс-таблица, дающая оптимальное решение, причем в этой таблице все искусственные элементы являются свободными, то отбросив столбцы для этих переменных, получим симплекс-таблицу, дающую оптимальное решение исходной задачи.
При решении М-задачи могут представиться две возможности:
1. М-задача имеет решение, если все искусственные элементы выведены из базиса.
2. Задача не имеет решение
- если вывели искусственные переменные и задача, решаемая симплекс-методом не имеет решения
- если при решении М-задачи получена симплекс-таблица, дающая при всех достаточно больших значениях М оптимальное решение и в этой таблице хотя бы одна искусственная переменная yi входит в базис, причем в строке для yi свободный член положителен, то исходная задача не имеет ни одного допустимого решения.
Решая М-задачу мы стремимся получить оптимальное решение, в котором значение исходных неизвестных равны 0. Для того чтобы этого достичь, необходимо выбрать последовательность шагов таким образом, чтобы все искусственные неизвестные вышли из базиса, т.е. стали свободными, тогда в базисном решении значения этих неизвестных будут нулями, т.о. переходя от одного базиса к другому мы стараемся в первую очередь выводить из базиса одно искусственное неизвестное за другим.
Возможны и такие случаи, когда в процессе решения приходиться заменять одно искусственное неизвестное на другое, т.к. выбор разрешающего элемента по другому не получается, но общим направлением вычислительного процесса во всех случаях остается постепенный вывод искусственных переменных из базиса.
f(x) = 2x1 + x2 – x3 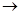 min
min
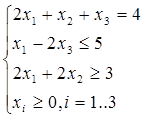
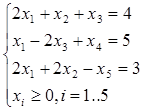
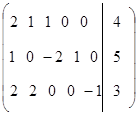
Вводим искусственные переменные
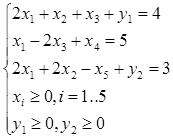
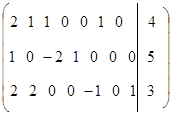
f(x) = 2x1 + x2 – x3+ My1 + My2 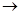 min
min
| -2 | -1 | M | M | ||||||
| Базовые переменные | Сводные члены | x1 | x2 | x3 | x4 | x5 | y1 | y2 | |
| M | y1 | ||||||||
| x4 | -2 | ||||||||
| M | y2 | 3/1.5 | 2/1 | 2/1 | 0/0 | -1/-0.5 | 1/0.5 | ||
| f(x) | 7M | 4M+2 | 3M-1 | M+1 | -M |
| -2 | -1 | M | M | ||||||
| Базовые переменные | Сводные члены | x1 | x2 | x3 | x4 | x5 | y1 | y2 | |
| M | y1 | -1 | -1 | ||||||
| x4 | 3.5 | -1 | -2 | 0.5 | -0.5 | ||||
| -2 | x1 | 1.5 | -0.5 | 0.5 | |||||
| f(x) | M-3 | -M-3 | M+1 | M+1 | -2M-1 |
| -2 | -1 | ||||||||
| Базовые переменные | Сводные члены | x1 | x2 | x3 | x4 | x5 | |||
| -1 | x3 | -1 | |||||||
| x4 | 5.5 | -3 | 2.5 | ||||||
| -2 | x1 | 1.5 | -0.5 | ||||||
| f(x) | -4 | -2 |
Ответ: f(x)min = -4, при
х1 = 1,5
х2 = 0
х3 = 1
х4 = 5,5
х5 = 0
Дата добавления: 2015-05-13; просмотров: 3496;
