Третья теорема двойственности (теорема об оценках).
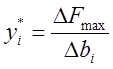
Объективно-обусловленные оценки ресурсов показывают насколько денежных единиц измениться максимальная прибыль при изменении запаса соответствующего ресурса на одну единицу, в случае если 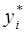 остается неизменной.
остается неизменной.
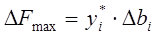
После того как оптимальное решение получено выявляется его чувствительность к определенным изменениям исходной модели, может представлять интерес, то как повлияет на оптимальное решение изменение запасов сырья в связи с этим необходимо получить ответы на следующие вопросы:
1. Увеличение объемов, какого вида ресурсов наиболее выгодно.
2. Насколько можно увеличить запас сырья для улучшения полученного оптимального значения целевой функции.
3. Целесообразность включения в план новых изделий.
Чувствительность решения к изменению запасов сырья.
Рассмотрим модель нашей задачи в матричной форме.
f(x) = cx 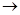 max, где
max, где
х = (х1,х2,…,хn) – вектор неизвестных
с = (с1,с2,…,сn) – вектор коэффициентов при неизвестных в целевой функции.
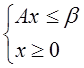 , где
, где 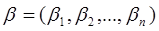 - вектор свободных членов системы ограничений исходной задачи.
- вектор свободных членов системы ограничений исходной задачи.
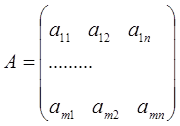 - матрица коэффициентов в системе ограничений.
- матрица коэффициентов в системе ограничений.
Приведем задачу к каноническому виду, т.е. введем m дополнительных переменных.
Задача принимает вид
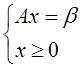 , где вектор неизвестных Х – будет теперь иметь размерность n+m, размерность матрицы А также измениться.
, где вектор неизвестных Х – будет теперь иметь размерность n+m, размерность матрицы А также измениться.
Пусть известен оптимальный план, разобьем наш вектор х на два подвектора
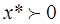 и х0 = 0
и х0 = 0
В первый включены неизвестные, вошедшие в базис оптимального решения, а вторые это свободные переменные, не вошедшие в базис.
Соответственно матрицу А тоже разобьем на две подматрицы А* размерность, которой (m 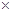 m) матрица которую формируют столбцы соответствующие не нулевым неизвестным в оптимальном плане. А0 (m
m) матрица которую формируют столбцы соответствующие не нулевым неизвестным в оптимальном плане. А0 (m 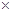 n) – ее формируют столбцы соответствующие нулевым неизвестным в оптимальном плане.
n) – ее формируют столбцы соответствующие нулевым неизвестным в оптимальном плане.
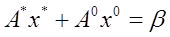
Так как 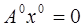 , то остается
, то остается
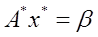

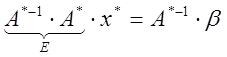
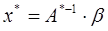
Пусть 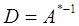 , тогда
, тогда
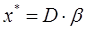
Матрица D характеризует влияние ресурсов на величину выпуска продукции Х.
Изменим размер выделенных ресурсов, т.е. дадим приращение 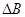 вектору В, тогда мы получим
вектору В, тогда мы получим
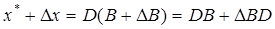
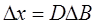
Это отношение определяет величину структурных сдвигов в выпуске продукции при изменении ограничений исходной задачи.
Из соотношений второй теоремы двойственности видно, что двойственные оценки тесным образом связаны с оптимальным планом исходной задачи, всякое изменении исходных данных прямой задачи может оказать влияние как на ее оптимальный план, так и на систему оптимальных двойственных оценок, поэтому чтобы проводить экономический анализ с использованием двойственных оценок нужно знать их интервал устойчивости.
Исходя из этого, мы имеем формулы дающие оценки нижних и верхних пределов устойчивости двойственных оценок при изменении каждого ограничения в отдельности, пределы уменьшения, т.е. нижняя граница, определяется по тем хк для которых
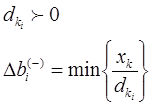
Пределы увеличения определяются по тем хк для которых
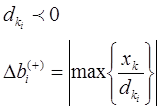
Определим интервал
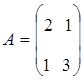
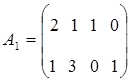
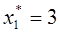
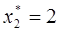
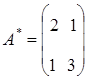
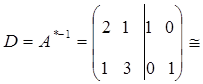
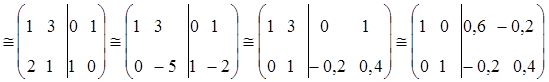
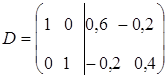
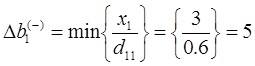
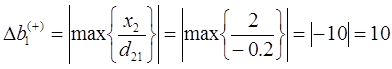
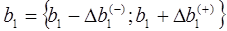
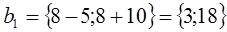
При изменении запасов ресурса S1 в пределах от трех до 18-ти единиц двойственная цена на него не меняется.
Найдем интервал устойчивости второго ресурса S2.
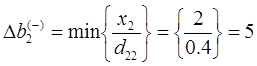
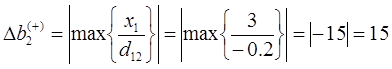
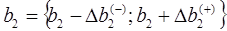
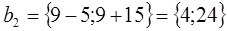
При изменении запасов ресурса S2 в пределах от 4 до 24 единиц двойственная оценка его не изменяется.
Задача №1.
На сколько измениться объем прибыли, если запас первого ресурса увеличиться на 2 единицы.
По третьей теореме двойственности
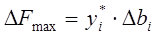
S1 = 8 + 2 = 10
это изменение находиться в интервалах устойчивости двойственных оценок, поэтому можно воспользоваться теоремой об оценках.
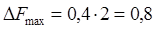
Прибыль увеличилась на 0,8 денежные единицы.
Задача №2.
На сколько измениться объем прибыли, если запас первого сырья увеличиться на 5 единиц, а запас второго сырья уменьшиться на 3 единицы одновременно.
S1 = 8 + 5 = 13
S2 = 9 – 3 = 6
Оба изменения находятся в интервалах устойчивости двух оценок, поэтому можно воспользоваться теоремой об оценках
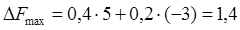
Объем прибыли увеличиться на 1,4 денежные единицы.
Задача №3. Целесообразность включения в план новых изделий.
Пусть в данной задаче предприятию были предложены на выбор 3 новых изделия, за счет которых можно было бы расширить номенклатуру выпускаемой продукции при тех же запасах ресурсов.
Нормы затрат ресурсов и прибыль от реализации единицы продукции для этих изделий представлены в таблице.
| Ресурсы | Обьективно-обусловленные оценки | Затраты ресурсов на 1 изделие | ||
| Т3 | Т4 | Т5 | ||
| S1 | 0,4 | |||
| S2 | 0,2 | |||
| Прибыль от реализации 1 шт. |
Третий товар
S1 = 8 – 4 = 4
S2 = 9 – 2 = 7
Данные значения попадают в интервалы устойчивости
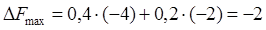
Сравниваем полученные затраты с прибылью от реализации одного изделия
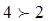 , затраты покрываются полученной прибылью, значит введение данного товара целесообразно.
, затраты покрываются полученной прибылью, значит введение данного товара целесообразно.
Четвертый товар
S1 = 8 – 2 = 4
S2 = 9 – 7 = 2 – не попадает в интервал
Значит, сами оценки могут измениться, поэтому нельзя решать задачу, используя третью теорему двойственности.
Пятый товар
S1 = 8 – 1 = 7
S2 = 9 – 4 = 5
Данные значения попадают в интервалы устойчивости
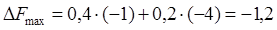
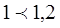 , затраты превышают прибыль, значит включать в план пятый товар не целесообразно.
, затраты превышают прибыль, значит включать в план пятый товар не целесообразно.
Дата добавления: 2015-05-13; просмотров: 1708;
