Взаимно-двойственные задачи линейного программирования.
С каждой задачей линейного программирования связана другая задача, называемая двойственной по отношению к исходной.
Совместное изучение данной и двойственной к ней задачи дает, как правило, значительно больше информации, чем изучение каждой из них в отдельности.
Постановка взаимно-двойственной задачи:
На некотором предприятии после выполнения годового плана возник вопрос, как поступить с остатками сырья, некоторые заводские экономисты предложили наладить из оставшегося сырья производство изделий ширпотреба, другие специалисты посоветовали продать сырье другой организации. Исследования этих двух возможностей поручили математикам, вывод, к которому они пришли, оказался неожиданным.
Пусть имеется 2 вида сырья S1 и S2 , остатки которого составляют
S1 = 8 ед. сырья
S2 = 9 ед.сырья
Из этого сырья можно наладить производство двух видов товара Т1 и Т2 о реализации каждого вида товара завод получает прибыль от Т1 – 1 руб./шт., от Т2 – 1 руб./шт. Нормы расхода сырья S1 на производство единицы товара Т1 составляют 2 единицы, а на производство Т2 – 1 единица. Расходы S2 на Т1 – 1 единица, S2 на Т2 – 3 единицы.
Прямая задача.
| Виды товара Виды ресурса | Т1 | Т2 | Запасы ресурсов |
| S1 | |||
| S2 | |||
| Прибыль от производства единицы товара |
х1 – оптимальное количество Т1
х2 – оптимальное количество Т2
f(x) = x1 + x2  max
max
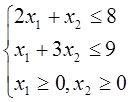
Двойственная задача.
у1 – цена единицы сырья S1
у2 – цена единицы сырья S2
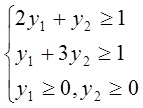
z(y) = 8y1 + 9y2  min
min
Вторая возможность продать сырье другой организации. Возникает вопрос, по каким ценам продавать сырье. Справедливое требование к ценам со стороны продающего предприятия состоит в следующем: если взять сырье, идущее на изготовление единицы товара Тi , то выручка от его продажи должна быть не меньше, чем прибыль от реализации готового изделия, в другом случае нет необходимости продавать сырье.
Целевая функция рассматривается с точки зрения покупателя, т.е. сокращения до минимума расходов на покупку сырья.
Под у1 и у2 понимаются не рыночные цены, а цены для внутреннего пользования предприятия или «объективно-обусловленные оценки».
Если к двойственной задаче снова построить двойственную задачу, то получим исходную задачу.
Не одна из двойственных задач не является основной, т.е. если поставлена одна из задач, то другая может быть сформулирована как двойственная и каждая из них является двойственной по отношению к другой.
Решим обе задачи графически.
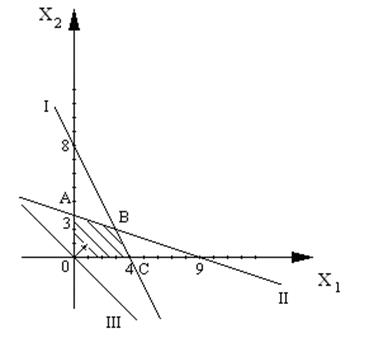
В – точка максимума
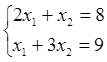
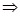 х1 = 3, х2 = 2
х1 = 3, х2 = 2
f(x)max = 3 + 2 = 5
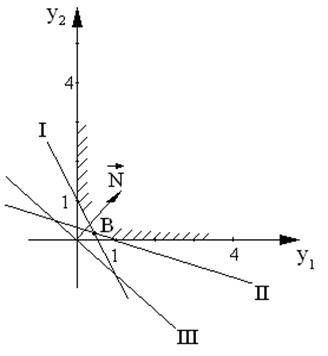
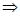 у1 = 0,4; у2 = 0,2
у1 = 0,4; у2 = 0,2
В(0,4;0,2)
z(y)min = 8*0.4 + 9*0.2 = 5
f(x)max = z(y)min = 5
Первая теорема двойственности: Если одна и взаимно-двойственных задач имеет оптимальный план, то другая тоже имеет оптимальный план, при этом значения целевых функций равны друг другу.
Первую и вторую задачу можно сравнить друг с другом. Обе задачи обладают следующими свойствами:
1. В одной задаче ищут максимум линейной функции, а в другой минимум.
2. Коэффициенты при переменных в линейной функции одной задачи являются свободными членами системы ограничений в другой.
3. Обе задачи в стандартном виде, причем в задаче максимизации все неравенства вида « 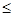 », а в задаче минимизации – «
», а в задаче минимизации – « 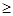 ».
».
4. Если мы построим матрицу исходной задачи из коэффициентов при переменных, расширим ее столбцом свободных членов прямой задачи и внизу припишем строку из коэффициентов целевой функции прямой задачи, то у нас транспонированная матрица прямой задачи будет равна матрице двойственной задачи.
5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.
6. Условия неотрицательности переменных имеются в обеих задачах.
Две задачи линейного программирования, обладающие указанными свойствами, называются симметричными взаимно-двойственными задачами.
Исходя из определения, можно предложить следующий алгоритм составления взаимно-двойственной задачи:
1. Привести все неравенства системы ограничений исходной задачи к одному смыслу. Если в исходной задаче ищут максимум линейной функции, то все неравенства системы ограничений привести к виду «меньше либо равно», а если минимум, то к виду «больше, либо равно», для этого неравенства, в которых данное требование не выполняется умножить на -1.
2. Составить расширенную матрицу системы А1, в которую включить матрицу при переменных, а столбец свободных членов системы ограничений и строку коэффициентов при переменных в линейной функции записать справа и снизу соответственно.
3. Найти матрицу, 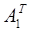 транспонированную к матрице А1.
транспонированную к матрице А1.
4. Сформировать взаимно-двойственную задачу на основании полученной матрицы 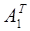 и условиях неотрицательности переменных.
и условиях неотрицательности переменных.
Исходная задача
f (x) = -x1 + 2x2 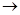 max
max
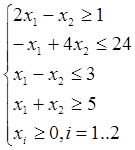
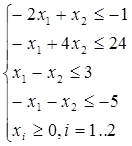
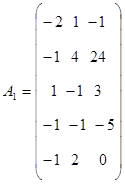
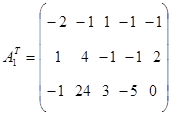
z(y) = -y1 + 24y2 + 3y3 – 5y4 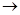 min
min
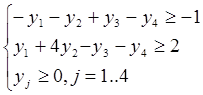
Первая теорема двойственности позволяет найти оптимальное значение двойственной задачи не решая ее.
Если в оптимальном плане одной из взаимно-двойственных задач значение основной переменной положительно, то соответствующая ей вспомогательная переменная другой задачи равна 0 и, наоборот, из положительности вспомогательной переменной следует равенство 0 соответствующей ей основной переменной в оптимальном плане взаимно-двойственой задачи.
Сделаем некоторые преобразования.
1. Приведем обе задачи к каноническому виду; запишем это преобразование в общем виде
Прямая задача
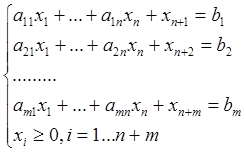
Двойственная задача
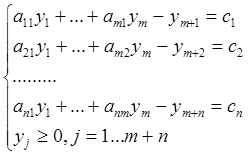
Прямая задача
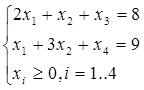
Двойственная задача
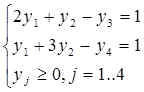
Системы линейных уравнений содержат m+n неизвестных в первой из них n основных переменных и m вспомогательных переменных, а во второй наоборот m основных переменных, n вспомогательных переменных.
Составим таблицу соответствия переменных в двух задачах
| I | Основные переменные | Вспомогательные переменные |
   x1, x2, … xn x1, x2, … xn
|   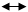 xn+1, xn+2, … xn+m xn+1, xn+2, … xn+m
| |
| II | ym+1, ym+2, … ym+n | y1, y2, … ym |
| Вспомогательные переменные | Основные переменные |
Соответствие между переменными не меняется при решении задачи
Для рассматриваемой задачи
| I | Основные переменные | Вспомогательные переменные |
3 2
  x1, x2 x1, x2
| 0 0
  x3, x4 x3, x4
| |
| II | y3, y4 0 0 | y1, y2 0,4 0,2 |
| Вспомогательные переменные | Основные переменные |
х3 = 8 – (2х1 + х2)
х4 = 9 – (х1 + 3х2)
у3 = (2у1 + у2) – 1
у4 = (у1 +3у2) – 1
Вторая теорема двойственности: компоненты оптимального решения взаимно-двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных линейной функции исходной задачи выраженной через не основные компоненты ее оптимально решения.
Если мы получили значения основных переменных не нулевыми, то у нас нет превышения затрат на ресурсы над ценой реализации, поэтому ресурсы дефицитные и условные цены на них равны не нулевые.
Если мы имеем основные переменные нулевые, то мы имеем превышение затрат на ресурсы над ценой их реализации, т.е. имеем объективно-обусловленные оценки равные нулю.
Решаем прямую задачу симплекс-методом
f(x) = x1 + x2 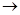 max
max
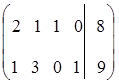
- f(x) = - x1 - x2 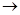 min
min
| -1 | -1 | ||||||
| Базовые переменные | Сводные члены | x1 | x2 | x3 | x4 | ||
| х3 | -1 | ||||||
| x4 | 9/3 | 1/ 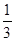
| 3/1 | 0/0 | 1/ 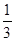
| 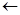
| |
| f(x) | |||||||
|
| -1 | -1 | ||||||
| Базовые переменные | Сводные члены | x1 | x2 | x3 | x4 | ||
| х3 | 5/3 | 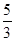 /1 /1
| 1/ 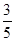
| - 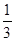 /-5 /-5
| 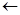
| ||
| -1 | x2 | 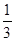
| 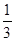
| ||||
| f(x) | -3 | 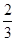
| - 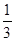
| ||||
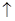
|
| -1 | -1 | ||||||
| Базовые переменные | Сводные члены | x1 | x2 | x3 | x4 | ||
| -1 | х1 | 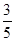
| -5 | ||||
| -1 | х2 | - 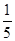
| 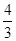
| ||||
| f(x) | -5 | - 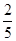
| - 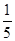
| ||||
f(x)max = 5, при
х1 = 3
х2 = 2
х3 = 0
х4 = 0
f(x)max = z(y)min = 5
Дата добавления: 2015-05-13; просмотров: 2188;
