Проектирование FIR фильтра на основе аппроксимации

Рассмотрим симметрический фильтр с передаточной функцией

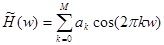. (1)

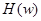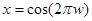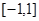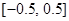Пусть задана вещественная передаточная функция . Положим . В результате замены имеем взаимно однозначное соответствие между точками интервалов и . Функции. 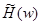, 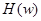преобразуются в функции 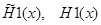соответственно. Известно, что существует разложение 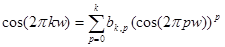. В результате получаем задачу аппроксимации вещественной функции 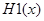с помощью многочлена 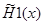степени не выше, чем 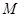. Построив многочлен, можем вернуться к представлению (1) заменой переменных и разложением в ряд Фурье.

Аппроксимацию указанного вида используют в случае, когда критерием является не средне квадратическое отклонение, а критерий типа 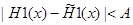. В этом случае применяется теория аналогичная теории многочленов Чебышева с наименьшими отклонениями. Задача решается приближенно. После того, как многочлен найден, возвращаемся к представлению (1).