Шкалирование
Рассмотрим множество функций 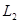 на вещественной оси. Пусть
на вещественной оси. Пусть 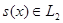 , причем функции
, причем функции 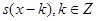 образуют ортонормированную систему. Это означает, что
образуют ортонормированную систему. Это означает, что
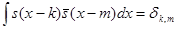 (2)
(2)
Такую функцию назовем шкалирующей. Например, любая функция, имеющая носитель внутри единичного интервала и норму равную 1, удовлетворяет условию (2). Обозначим через 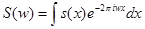
Предложение. Имеет место формула
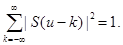 (3).
(3).
Обратно, из (3) следует (2)
Доказательство. Имеем 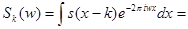
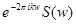 . Поскольку преобразование Фурье является ортогональным преобразованием,
. Поскольку преобразование Фурье является ортогональным преобразованием, 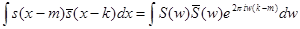 . С учетом (2) это означает, что
. С учетом (2) это означает, что 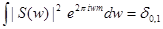 . Далее, пусть
. Далее, пусть 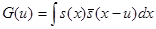 . Преобразование Фурье этой функции есть
. Преобразование Фурье этой функции есть 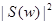 . Теперь
. Теперь 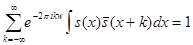 , так как остальные слагаемы равны нулю в силу (2). Заменим сумму интегралом и продолжим равенство
, так как остальные слагаемы равны нулю в силу (2). Заменим сумму интегралом и продолжим равенство 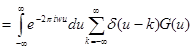 . Заменим преобразование Фурье от произведения сверткой их образов. Преобразование от первого сомножителя есть он сам. Таким образом, равенство продолжается
. Заменим преобразование Фурье от произведения сверткой их образов. Преобразование от первого сомножителя есть он сам. Таким образом, равенство продолжается 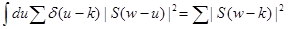 . Обратное утверждение доказывается переписыванием формул в обратном порядке.
. Обратное утверждение доказывается переписыванием формул в обратном порядке.
Важным примером материнской функции является функция, равная 1 на интервале 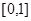 и 0 в остальных точках. Такую функцию обозначим через
и 0 в остальных точках. Такую функцию обозначим через 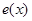 .
.
Задача. Найти явный вид формулы (2) для функции 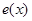 .
.
Дата добавления: 2015-05-13; просмотров: 1106;
