Детализация сигнала

Введем обозначение: 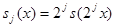для любой функции 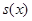. Положим .

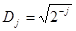Предложение. Если выполнено условие ортогональности, то при фиксированном 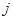функции 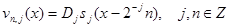образуют ортонормированную систему.

Доказательство. Имеем

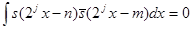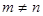при . Нормированность проверяется очевидным образом с помощью замены переменных.

Обозначим через 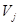линейное пространство, порожденное функциями 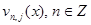. Потребуем, чтобы имело место включение . Это весьма жесткое ограничение. Оно выполнено, например, для 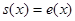. Для произвольной функции 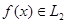положим

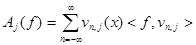(1)

- проекция функции на пространство 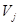. Коэффициенты разложения это и есть дискретные wavelet преобразования. Чем больше индекс пространства, тем более точное приближение исходной функции с помощью 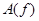получаем. Эта процедура и называется детализацией. Наложим на 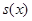еще одно дополнительное условие: потребуем, чтобы 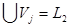. Последнее означает, что каждую функцию из 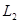можно приблизить с произвольной точностью подходящей функцией из 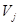. Заметим, что это выполнено для функции 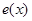, поскольку каждую функцию из 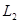можно приблизить ступенчатой функцией. Как следствие получим, что это верно и для произвольной функции с носителем на интервале 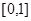, с помощью которой можно приблизить функцию 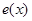. Положим 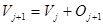, где второе слагаемое есть ортогональное дополнение к первому. Теперь 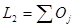- прямая сумма попарно ортогональных пространств. Для 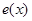так получается базис Хаара, о котором будет рассказано позже.