И решетчатая диаграмма сигнала ГММС

При когерентной демодуляции в приемнике любого радиосигнала обычно сначала из принимаемого колебания (смеси сигнала и помехи на входе приемника) выделяют комплексную огибающую, из значений которой затем выделяют информационные символы. Если при этом используется корреляционный способ выделения (демодуляции), то в приемнике необходимо иметь возможность формировать копии возможных вариантов комплексной огибающей переданного радиосигнала на каждом текущем интервале времени .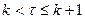

К сожалению для сигнала ГММС значения сигнала на текущем интервале зависят от всех предшествующих информационных символов. Тем не менее восстановить все возможные траектории (реализации) сигнала ГММС на каждом очередном интервале времени 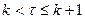можно, если учесть особенности его комплексной огибающей, определяемой равенствами (11) и (15). Действительно, подставляя (11) в (15), можно записать для интервала :

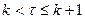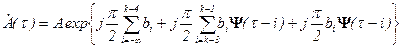Первое слагаемое в показателе комплексной экспоненты представляет собой независящую от времени долю фазы комплексной огибающей на текущем интервале; второе слагаемое является функцией времени и полностью определяется тремя предшествующими символами; наконец последнее слагаемое есть вклад текущего информационного символа в значения фазы на данном интервале.

Очевидно, что множитель 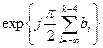принимает значения из множества 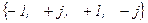, т.е. значение показателя этой экспоненты можно вычислять по модулю 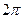, так что возможные его значения принадлежат множеству 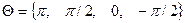. В результате комплексную огибающую сигнала ГММС на интервале с номером 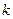можно представить выражением:

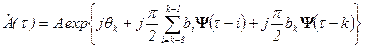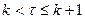, . (16)

Это выражение можно записать в более простой и удобной для последующего моделирования на ПЭВМ форме, если ввести следующие обозначения:

, ; , ;

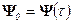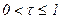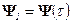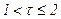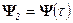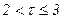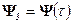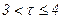, ; , . (17)

Теперь вместо (16) можно записать:

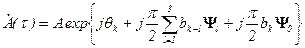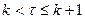, . (18)

Представление (18) комплексной огибающей ГММС сигнала можно положить в основу построения функциональной схемы устройства формирования этого сигнала, которая представлена на рис. 5. Здесь регистр сдвига с элементами задержки на время 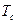связан через устройства умножения с сумматором функций 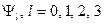. На выходе этого сумматора формируется меняющаяся во времени доля фазы сигнала. Во втором сумматоре накапливается неменяющаяся на этом интервале доля фазы.

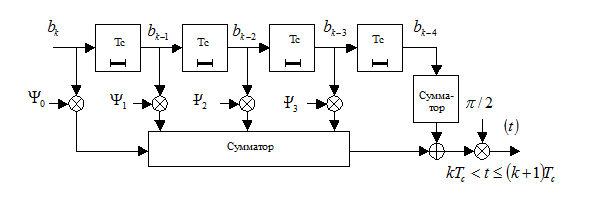
Рис. 5. Устройство формирования фазы сигнала ГММС

Такое представление позволяет построить решетчатую диаграмму состояний сигнала ГММС, с помощью которой сравнительно легко можно рассчитывать значения комплексной огибающей этого сигнала на любом интервале времени с номером 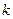, если известно значение вектора состояния 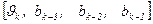устройства формирования ГММС сигнала и значение 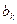символа на входе устройства на текущем интервале. В установившемся режиме диаграмма представляется периодической структурой, один элемент которой представлен на рис. 6.

Из этого рисунка следует, что число разных состояний равно 32, а число возможных переходов равно 64; не все переходы изображены на рисунке, чтобы не загромождать рисунок. Сплошные стрелки соответствуют переходам, если на k-том интервале символ 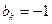, переходы при 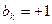изображены пунктирными стрелками.

Построение фазовой траектории сигнала ГММС на интервале 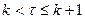теперь осуществляется следующим образом. Предполагаются известными значения вектора [ 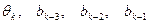] и, следовательно, состояние слева на решетке. При появлении символа 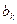его значение становится известным. Теперь значения комплексной огибающей можно вычислить по формуле (18) для всех моментов времени интервала с номером 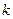. К моменту окончания этого интервала завершается переход по решетке в новое состояние для интервала с номером 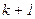, которое теперь определяется новым вектором [ 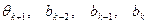], где 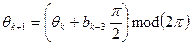. Решетка определяет все возможные переходы для любых возможных значений вектора [ 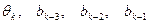] и двух возможных значений текущего символа 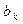. В результате оказывается возможным вычислить все возможные траектории (реализации) комплексной огибающей сигнала ГММС на этом интервале (для всех возможных значений вектора состояния), что необходимо для формирования опорного сигнала при когерентном способе демодуляции этого сигнала.

Отметим, в заключение, что данная решетчатая диаграмма оказывается полезной при реализации алгоритма «приема сигнала в целом», так как обеспечивает возможность использования алгоритма Витерби, который обладает существенно меньшей вычислительной сложностью по сравнению с традиционным алгоритмом максимального правдоподобия.

Рис. 6. Решетчатая диаграмма сигнала ГММС

Для GmSK обычно используют одну из двух схем модуляции - C управляемым по частоте генератором (УГ) и квадратурным модулятором, которые в упрощённом виде показаны на рис. 22.

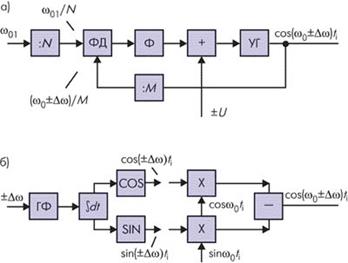
Рисунок 22 - Схемы GmSK модуляторов

В модуляторе с УГ рис. 1а используется система ФАПЧ, обеспечивающая высокую стабильность несущей частоты ЧМ (ЧМн) сигнала. При этом собственно модулятором является УГ, а система ФАПЧ обеспечивает получение несущей, равной = (m/N) 01. m и N - это коэффициенты деления частоты в делителях ":m" и ":N", а 01 - стабильная частота опорного источника. Делители используются для точной настройки на требуемую частоту В этом смысле модулятор по схеме на рис. 1а является одновременно синтезатором частот типа "INteGeR-N".

Модулятор характеризуется передаточной функцией

Kмод(P) = KУГ/[1 + KФ(P)/P 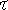0], (1)

где KУГ - коэффициент преобразования УГ (с размерностью (рад/с)/В), 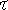0 = m/KУГKФДKФ - постоянная времени, KФД - коэффициент передачи фазового детектора ФД, KФ и KФ(P) - постоянный и частотно-зависимый множители передаточной функции фильтра. Согласно (1), модулятор обладает свойствами фильтра верхних частот. Это соответствует используемым кодовым последовательностям модулирующего сигнала (без постоянной составляющей).

Модулятор по схеме рис. 22а является, по существу, аналоговым, используемым для манипуляции. Обозначения, приведённые на рис. 1а (и на других рисунках), например, Cos( 0± 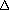)tI, являются упрощёнными и, строго говоря, соответствуют установившимся значениям частоты посылок (то есть без учёта переходных процессов, связанных с изменением частоты ± ).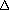

Модулятор GmSK с УГ по схеме на рис. 22а применяется обычно в беспроводной телефонии (в системе DECT), а в системе GSM применяется квадратурный модулятор, схема которого приведена на рис. 22б. Собственно квадратурный модулятор содержит перемножители с опорными источниками Cos 0tI и sIN 0tI и вычитатель на выходе. На вход перемножителей поступают две составляющие квадратурного сигнала Cos(± 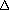)tI и sIN(± 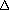)tI, формируемые обычно в DSP. При этом, если модулятор аналоговый, на выходе DSP используют ЦАП. Квадратурный модулятор может быть цифровым и иметь ЦАП на своём выходе [7]. На рис. 22б показаны эквивалентные цепи DSP - гауссовский фильтр ГФ, интегратор 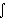dt и элементы тригонометрических функций "Cos" и "sIN". На вход поступает нефильтрованная последовательность положительных и отрицательных значений "±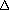 ", соответствующая "1" и "0" модулирующего кода. Указанная последовательность фильтруется в ГФ. Её фронты сглажены, а частотный спектр, соответственно, сужен.

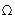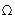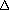
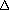
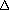
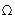На рис. 23 приведены схемы квадратурных модуляторов, совмещённых с повышающим преобразователем частоты: 0 = 01 + 02, где 0 - несущая ВЧ, 01 - несущая на выходе модулятора, определяемая частотой первого гетеродина, 02 - частота второго гетеродина. Показанные на входе Cos tI и ±sINt tI, которые более наглядны, соответствуют Cos(± )tI и sIN(± )tI на рис. 1б (при = ). Схема устройства на рис. 23апроще, чем на рис. 23б, и содержит последовательно включённые модулятор и преобразователь частоты. Преобразователь построен с использованием системы ФАПЧ и дополнительно содержит смеситель (перемножитель) и фильтр Ф2. Фильтр пропускает составляющие с несущей 01, равной разности 0 – 02, и подавляет составляющие с 0 + 02. Фильтр Ф2 не является обязательным, если, например, смеситель выполнен по балансной схеме.

123 4

Дата добавления: 2015-05-28; просмотров: 1376;