Фильтр Гаусса; Функциональная схема Модулятора.
Имитатор сигнала стандарта GSM
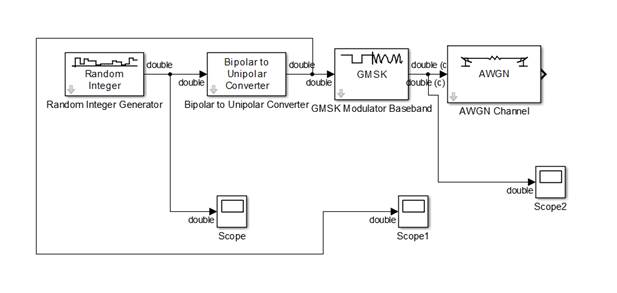
Фильтр Гаусса; Функциональная схема Модулятора.
Фильтр Гаусса — электронный фильтр, чьей импульсной переходной функцией является функция Гаусса. Фильтр Гаусса спроектирован таким образом, чтобы не иметь перерегулирования в переходной функции и максимизировать постоянную времени. Такое поведение тесно связано с тем, что фильтр Гаусса имеет минимально возможную групповую задержку.
Фильтр Гаусса (Gaussian filter) обычно используется в цифровом виде
 для обработки двумерных сигналов (изображений) с целью снижения уровня шума. Однако при ресемплинге он дает сильное размытие изображения.
для обработки двумерных сигналов (изображений) с целью снижения уровня шума. Однако при ресемплинге он дает сильное размытие изображения.
Кроме того, этот фильтр используется для получения гауссовской модуляции. Этот вид модуляции применяется в системе сотовой связи GSM.
Стандартом GSM предусматривается формирование радиосигнала со специальным видом модуляции, который принято называть гауссовской модуляцией с минимальным сдвигом (ГММС). Радиосигнал при такой модуляции имеет пониженный уровень внеполосных излучений, что позволяет располагать частотные каналы ближе друг к другу, обеспечивая более высокую спектральную эффективность системы связи. Функциональная схема устройства формирования этого сигнала представлена на рис. 1.
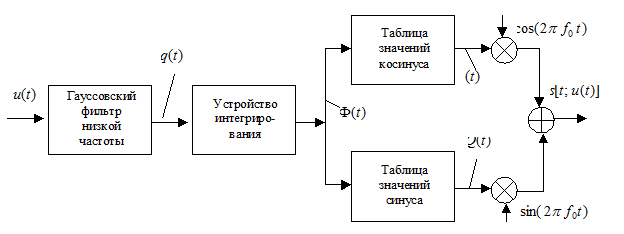 Рис. 1. Функциональная схема устройства формирования сигнала ГММС
Рис. 1. Функциональная схема устройства формирования сигнала ГММС
На вход модулятора подается модулирующий сигнал
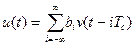 ,
, 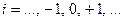 (1)
(1)
где 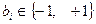 - информационный символ, формируемый источником информации на интервале времени
- информационный символ, формируемый источником информации на интервале времени 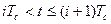 с номером
с номером  ,
, 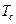 - длительность информационного символа, функция
- длительность информационного символа, функция
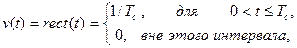 (2)
(2)
определяет форму этого символа. Сигнал (1) подвергается предварительной низкочастотной фильтрации с помощью гауссовского фильтра низкой частоты, который должен иметь импульсный отклик следующей формы
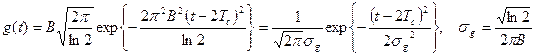 , (3)
, (3)
где 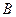 - ширина полосы пропускания этого фильтра на уровне 0,707 от максимального значения его амплитудно-частотной характеристики
- ширина полосы пропускания этого фильтра на уровне 0,707 от максимального значения его амплитудно-частотной характеристики
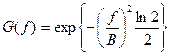 . (4) Из этого выражения следует, что физически реализуемый фильтр не может иметь такой импульсный отклик, поскольку его значения при отрицательном значении аргумента
. (4) Из этого выражения следует, что физически реализуемый фильтр не может иметь такой импульсный отклик, поскольку его значения при отрицательном значении аргумента 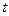 отличны от нуля, т.е. отклик фильтра появляется на выходе фильтра раньше начала воздействия на входе. Тем не менее можно считать, что такой фильтр может быть реализован приближенно, т.е. импульсный отклик физически реализуемого фильтра достаточно хорошо можно аппроксимировать функцией
отличны от нуля, т.е. отклик фильтра появляется на выходе фильтра раньше начала воздействия на входе. Тем не менее можно считать, что такой фильтр может быть реализован приближенно, т.е. импульсный отклик физически реализуемого фильтра достаточно хорошо можно аппроксимировать функцией 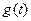 для
для 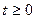 .
.
При моделировании более удобно использовать нормированное время 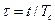 , при котором из (3) получаем:
, при котором из (3) получаем:
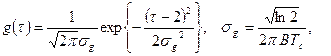
 . (5)
. (5)
Единственным параметром такого представления является произведение 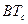 полосы пропускания фильтра на длительность прямоугольного импульса на его входе. Длительность символа в стандарте GSM-900 принята равной
полосы пропускания фильтра на длительность прямоугольного импульса на его входе. Длительность символа в стандарте GSM-900 принята равной  мкс и не может быть изменена. Значение полосы пропускания фильтра
мкс и не может быть изменена. Значение полосы пропускания фильтра 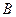 может быть выбрано из разных соображений. Стандартом GSM-900 рекомендуется значение произведения
может быть выбрано из разных соображений. Стандартом GSM-900 рекомендуется значение произведения 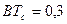 . График функции (5) при
. График функции (5) при 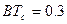 изображен на рис. 2.
изображен на рис. 2.
Отклик гауссовского фильтра на воздействие в виде одиночного прямоугольного импульса (2) вычисляется как свертка этого импульса и отклика (5):
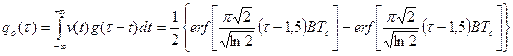 ,
, 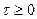 . (6)
. (6)
График этого отклика представлен на рис. 3. Важно здесь обратить внимание, что одиночный прямоугольный импульс на входе фильтра имеет длительность 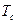 , а отклик на выходе фильтра заметно отличен от нуля на интервале
, а отклик на выходе фильтра заметно отличен от нуля на интервале 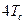 . В результате соседние символы на выходе гауссовского фильтра существенно перекрываются, т.е. имеет место межсимвольная интерференция (МСИ).
. В результате соседние символы на выходе гауссовского фильтра существенно перекрываются, т.е. имеет место межсимвольная интерференция (МСИ).
Теперь очевидно, что если модулирующий сигнал (1) подать на вход ГФНЧ, то сигнал на его выходе можно представить как сумму сверток (6):
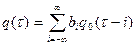 ,
, 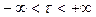 . (7)
. (7)
Следовательно, сигнал на выходе устройства интегрирования на бесконечном интервале времени  можно записать в виде следующей суммы:
можно записать в виде следующей суммы:
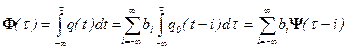 ,
,  . (8)
. (8)
Здесь введено обозначение
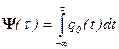 ,
,  , (9)
, (9)
для интеграла от одиночного отклика гауссовского фильтра, которое обычно называют фазовой функцией. График этой функции для случая, когда функция  имеет вид, представленный на рис. 3, изображен на рис. 4.
имеет вид, представленный на рис. 3, изображен на рис. 4.
Здесь важно отметить, что значения фазовой функции изменяются только на интервале 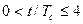 , длительность которого равна 4-м длительностям информационного символа. Вне этого интервала значения этой функции равны либо 0, либо 1.
, длительность которого равна 4-м длительностям информационного символа. Вне этого интервала значения этой функции равны либо 0, либо 1.
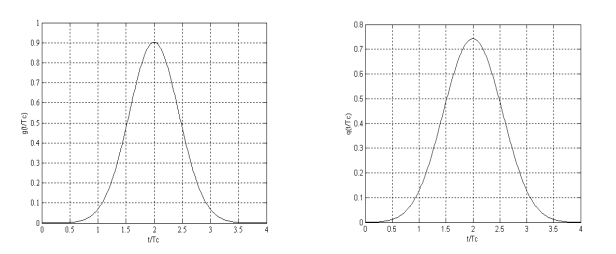
| Рис. 2. Импульсный отклик гауссовского фильтра низкой частоты | Рис. 3. Отклик гауссовского фильтра на одиночный прямоугольный импульс длительностью Tc |
В дальнейшем нам потребуется представление функции (8) на конечном интервале времени 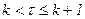 , на котором на входе модулятора действует информационный символ с номером
, на котором на входе модулятора действует информационный символ с номером 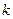 . В соответствии с (8) сначала можно записать выражение
. В соответствии с (8) сначала можно записать выражение
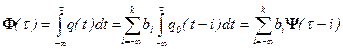 ,
, 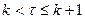 , (10)
, (10)
в котором учитывается, что мы не рассматриваем символы со значениями индекса  , превышающими значение
, превышающими значение 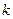 . Однако это выражение можно записать в более простой форме, если учесть, что символы на прошлых интервалах времени вносят разные вклады в значения функции
. Однако это выражение можно записать в более простой форме, если учесть, что символы на прошлых интервалах времени вносят разные вклады в значения функции 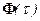 на рассматриваемом интервале с номером
на рассматриваемом интервале с номером 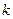 . Действительно, из рис. 4 следует, что все информационные символы со значениями индекса
. Действительно, из рис. 4 следует, что все информационные символы со значениями индекса 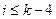 добавляют в выражение (10) только +1 или –1 в соответствии со значениями символов
добавляют в выражение (10) только +1 или –1 в соответствии со значениями символов 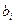 . Вклад трех предшествующих символов можно представить слагаемым
. Вклад трех предшествующих символов можно представить слагаемым 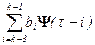 . Тогда вместо (10) можно записать:
. Тогда вместо (10) можно записать:
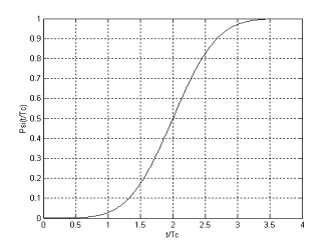
Рис. 4. Фазовая функция сигнала ГММС при BTc=0,3
 ,
, 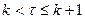 . (11)
. (11)
Значением первого слагаемого в правой части равенства здесь может оказаться любое целое число, положительное или отрицательное, включая 0. Два последних слагаемых определяют изменение функции 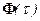 на интервале с номером
на интервале с номером 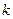 .
.
Таким образом, сигнал на выходе устройства интегрирования обладает «памятью» - значения этого сигнала на интервале с номером 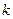 зависят от информационных символов на всех предшествующих интервалах времени.
зависят от информационных символов на всех предшествующих интервалах времени.
Теперь возвращаемся к схеме устройства, представленной на рис. 1, в соответствии с которой над сигналом 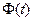 одновременно выполняются следующие преобразования:
одновременно выполняются следующие преобразования:
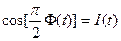 ,
, 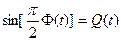 . (12)
. (12)
Функции (12) называются квадратурными компонентами сигнала ГММС. В результате радиосигнал на выходе модулятора теперь принимает вид:
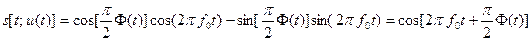 . (13)
. (13)
В этих выражениях добавлен множитель 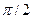 для того, чтобы полное приращение фазы сигнала, обусловленное одним информационным символом, было равно
для того, чтобы полное приращение фазы сигнала, обусловленное одним информационным символом, было равно 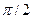 , как это имеет место для сигнала с модуляцией минимального сдвига (ММС). Именно благодаря этому свойству сигнал (13) назван сигналом с минимальным сдвигом.
, как это имеет место для сигнала с модуляцией минимального сдвига (ММС). Именно благодаря этому свойству сигнал (13) назван сигналом с минимальным сдвигом.
На рис. 1 не указан усилитель мощности, который является обязательным функциональным элементом радиопередатчика. Усиление сигнала (13) выполняется таким образом, чтобы излучаемая антенной передатчика мощность сигнала имела вполне определенное значение, что является обязательным условием для сотовых систем. Поэтому для правильного представления о форме радиосигнала ГММС в (13) единичную амплитуду необходимо заменить на амплитуду 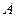 с определенным значением. В результате для сигнала ГММС мы получаем следующее общее представление:
с определенным значением. В результате для сигнала ГММС мы получаем следующее общее представление:
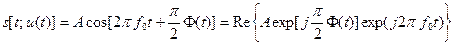 , (14)
, (14)
где 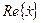 обозначает вещественную часть комплексной величины
обозначает вещественную часть комплексной величины 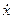 .
.
В соответствии с (14) радиосигнал ГММС является сигналом с угловой (частотной или фазовой) модуляцией и имеет постоянную огибающую. Если рассматривать значения этого сигнала на всех интервалах вплоть до текущего интервала с номером 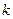 , то вся последовательность информационных символов
, то вся последовательность информационных символов 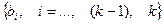 закодирована в значения функции
закодирована в значения функции 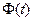 на этих интервалах. Поэтому комплексная огибающая сигнала ГММС
на этих интервалах. Поэтому комплексная огибающая сигнала ГММС
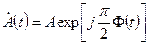 (15)
(15)
содержит в себе всю передаваемую информацию и определяет все свойства сигнала ГММС. Множитель 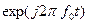 не зависит от последовательности информационных символов и определяет только несущее гармоническое колебание. Если функция
не зависит от последовательности информационных символов и определяет только несущее гармоническое колебание. Если функция 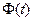 здесь определяется равенством (11), то (14) представляет радиосигнал ГММС, а (15) – его комплексную огибающую на интервале
здесь определяется равенством (11), то (14) представляет радиосигнал ГММС, а (15) – его комплексную огибающую на интервале 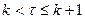 .
.
Дата добавления: 2015-05-28; просмотров: 3512;
