Непрерывное преобразование.

Пусть имеется функция 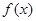и некоторая функция 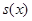- материнская функция. Рассмотрим числа вида

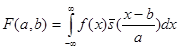(1)

Если 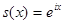, то в результате получаем обычное преобразование Фурье ( параметр 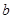не используется по понятной причине). Формула (1) определяет общее Wavelet преобразование. Существует формула обратного преобразования, позволяющая в некоторых случаях восстановить исходную функцию по ее преобразованию. Однако основной смысл преобразования (1) заключается в другом. Величина 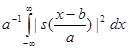не зависит от параметров. Это означает, что вектор, заданный функцией 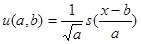, имеет постоянную длину в смысле пространства 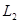. Предположим, что удалось найти такие значения параметров, для которых 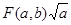достигает локального максимума. Это означает, что проекция функции 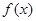на соответствующую функцию 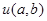имеет максимальное значение, поэтому графики этих функций аналогичны. Положив 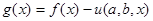, получим невязку, для которой решается такая же задача. В результате получаем приближение исходной функции функциями, порожденными с помощью функций 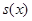. Это дает альтернативное описание исходной функции. В зависимости от того, какого рода особенности требуется обнаружить, выбирают вид материнской функции. При цифровой обработке, когда исходная функция задана лишь в отдельных точках, используется дискретное преобразование. Оказалось, что и в общем случае удается построить теорию, напоминающую теорию преобразования Фурье.

На практике, в качестве материнской фуекции при указанном подходе часто используют функцию 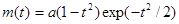( мексиканская шляпа). Константу 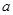определяют из условия нормировки